题目内容
某人身高1.8m,开始时站在路灯下的影子长为3.6m,然后他向路灯走近3.6m(指水平距离),此时他的影子长与身高相等.求路灯高,以及开始时他与路灯的水平距离.
考点:相似三角形的应用,中心投影
专题:
分析:根据题意画出图形,进而得出△E′F′D∽△ABD,△EFC∽△ABC,再利用相似三角性质求出即可.
解答: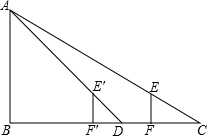 解:如图所示:由题意可得:EF=E′F′=1.8m,FF′=3.6m,F′D=1.8m,FC=3.6m,
解:如图所示:由题意可得:EF=E′F′=1.8m,FF′=3.6m,F′D=1.8m,FC=3.6m,
∵E′F′∥AB,EF∥AB,
∴△E′F′D∽△ABD,△EFC∽△ABC,
∴
=
,
=
,
设AB=x,BF′=y,
则
=
,
=
,
故
=
,
解得:y=3.6,则x=5.4,
故BF=3.6+3.6=7.2(m)
答:路灯高为5.4m,开始时他与路灯的水平距离为7.2m.
 解:如图所示:由题意可得:EF=E′F′=1.8m,FF′=3.6m,F′D=1.8m,FC=3.6m,
解:如图所示:由题意可得:EF=E′F′=1.8m,FF′=3.6m,F′D=1.8m,FC=3.6m,∵E′F′∥AB,EF∥AB,
∴△E′F′D∽△ABD,△EFC∽△ABC,
∴
| E′F′ |
| AB |
| F′D |
| BD |
| EF |
| AB |
| FC |
| BC |
设AB=x,BF′=y,
则
| 1.8 |
| x |
| 1.8 |
| 1.8+y |
| 1.8 |
| x |
| 3.6 |
| 3.6+3.6+y |
故
| 1.8 |
| 1.8+y |
| 3.6 |
| 3.6+3.6+y |
解得:y=3.6,则x=5.4,
故BF=3.6+3.6=7.2(m)
答:路灯高为5.4m,开始时他与路灯的水平距离为7.2m.
点评:此题主要考查了相似三角形的性质与判定,熟练应用相似三角形的性质是解题关键.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
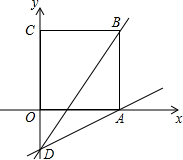 已知在平面直角坐标系中,点O为坐标原点,直线y=
已知在平面直角坐标系中,点O为坐标原点,直线y=
 如图,在Rt△ABC中,∠ACB=90°,BC=5,AC=12,CD⊥AB于点D
如图,在Rt△ABC中,∠ACB=90°,BC=5,AC=12,CD⊥AB于点D 如图:在Rt△ABC中,∠C=90°,D为AB的中点,DE⊥AB于D,交BC于点E,DE=CE,求∠B的度数.
如图:在Rt△ABC中,∠C=90°,D为AB的中点,DE⊥AB于D,交BC于点E,DE=CE,求∠B的度数.