Question

7．如图，在平面直角坐标系中，直线y=-2x+4与x轴、y轴分别相交于点A，B，四边形ABCD是正方形，曲线y=$\frac{k}{x}$在第一象限经过点D．将正方形ABCD沿x轴向左平移（　　）个单位长度时，点C的对应点恰好落在曲线上．

• A． $\frac{1}{2}$
• B． 1
• C． $\frac{3}{2}$
• D． 2

Answer 1

分析 作辅助线构建全等三角形，证明△AOB≌△DGA≌BFC，得出点D和点C的坐标，求出反比例函数的解析式，由题意可知C和E的纵坐标相等，从而求出点E的坐标，得出答案．

解答 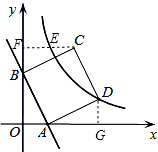解：过C作CF⊥y轴，交双曲线于点E，交y轴于点F，
过D作DG⊥x轴于G，
当x=0时，y=4，则OB=4，
当y=0时，x=2，则OA=2，
∵四边形ABCD是正方形，
∴AB=AD，∠BAD=90°，
∴∠BAO+∠DAG=90°，∠BAO+∠OBA=90°，
∴∠OBA=∠DAG，
∵∠AOB=∠AGD=90°，
∴△AOB≌△DGA，
∴AG=OB=4，DG=OA=2，
∴D（6，2），
∴k=2×6=12，
∴y=$\frac{12}{x}$，
同理得：△CFB≌△BOA，
∴CF=OB=4，BF=OA=2，
∴C（4，6），
当y=6时，x=2，
∴CE=CF-EF=4-2=2，
则将正方形ABCD沿x轴向左平移2个单位长度时，点C的对应点恰好落在曲线上．
故选D．

点评 本题是一次函数和反比例函数的综合，难度不大，但运用的性质较多，考查了利用待定系数法求函数的解析式，同时又能利用函数解析式求与坐标轴的交点坐标：①与x轴交点?令y=0，②与y轴交点?令x=0；运用三角形全等除了可以证明对应边相等外，还可以求出点的坐标，结合正方形性质，得出结论．