题目内容
9.若平面直角坐标系中,两点关于过原点的一条直线对称,则这两点就是互为镜面点,这条直线叫镜面直线,如A(2,3)和B(3,2)是以y=x为镜面直线的镜面点.(1)M(4,1)和N(-1,-4)是一对镜面点,则镜面直线为y=-x;
(2)以y=$\sqrt{3}$x为镜面直线,E(-2,0)的镜面点为(1,-$\sqrt{3}$).
分析 (1)求得线段MN的中点,然后根据待定系数法即可求得;
(2)根据题意求得经过E(-2,0)和它的镜面点的直线的解析式,然后联立方程求得交点坐标,根据轴对称的性质即可求得镜面点的坐标.
解答 解:(1)设直线MN的解析式为y=kx+b,
∵M(4,1)和N(-1,-4),
∴线段MN的中点为($\frac{3}{2}$,-$\frac{3}{2}$),
∵镜面直线经过原点和($\frac{3}{2}$,-$\frac{3}{2}$),
∴镜面直线为y=-x;
(2)∵y=$\sqrt{3}$x为镜面直线,
∴经过E(-2,0)和它的镜面点的直线为y=-$\frac{\sqrt{3}}{3}$x+b,
∴$\frac{2\sqrt{3}}{3}$+b=0,
∴b=-$\frac{2\sqrt{3}}{3}$,
∴y=-$\frac{\sqrt{3}}{3}$x-$\frac{2\sqrt{3}}{3}$,
解$\left\{\begin{array}{l}{y=\sqrt{3}x}\\{y=-\frac{\sqrt{3}}{3}x-\frac{2\sqrt{3}}{3}}\end{array}\right.$得$\left\{\begin{array}{l}{x=-\frac{1}{2}}\\{y=-\frac{\sqrt{3}}{2}}\end{array}\right.$,
设镜面点为(x,y),
∴$\frac{-2+x}{2}$=-$\frac{1}{2}$,$\frac{0+y}{2}$=-$\frac{\sqrt{3}}{2}$,
解得x=1,y=-$\sqrt{3}$,
∴镜面点为$(1,-\sqrt{3})$;
故答案为y=-x;(1,-$\sqrt{3}$).
点评 本题考查了一次函数图象与几何变换,熟练掌握轴对称的性质是解题的关键.

| A. | 2 | B. | ±2 | C. | ±4 | D. | 不存在 |
 如图,数轴上点P表示的数可能是( )
如图,数轴上点P表示的数可能是( )| A. | $\sqrt{2}$ | B. | $\sqrt{5}$ | C. | $\sqrt{10}$ | D. | $\sqrt{15}$ |
全国人口、儿童人口、儿科医生及每千名儿童拥有的儿科医生数统计表
| 年份 | 全国人口 (亿人) | 儿童人口 (亿人) | 儿科医生 (万人) | 每千名儿童拥有的儿科医生数 |
| 2000 | 12.67 | 2.9 | 9.57 | 0.33 |
| 2005 | 13.06 | 2.65 | 10.07 | 0.38 |
| 2010 | 13.4 | 2.22 | 10.43 | 0.47 |
| 2015 | 13.7 | 2.26 | 9.72 | 0.43 |
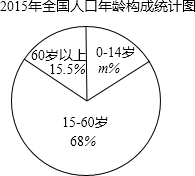
根据以上信息解答下列问题:
(1)直接写出扇形统计图中m的值;
(2)根据统计表估计2020年我国人口数约为14亿人;
(3)若2020年我国儿童占总人口的百分比与2015年相同,请你估算到2020年我国儿科医生需比2015年增加多少万人,才能使每千名儿童拥有的儿科医生数达到0.6.
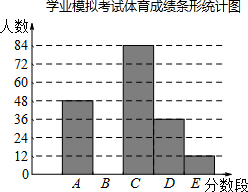 为迎接2016年贵阳市初中毕业生学业体育考试,某校进行了九年级学生学业考试体育模拟考试.为了解本次模拟考试的成绩(分数为整数)情况,现从中随机抽取部分学生的体育成绩分为五个等级,其中A:50分;B:49-45分;C:44-40分;D:39-30分;E:29-0分.根据所分等级情况制作了如下两个不完整的统计图表:
为迎接2016年贵阳市初中毕业生学业体育考试,某校进行了九年级学生学业考试体育模拟考试.为了解本次模拟考试的成绩(分数为整数)情况,现从中随机抽取部分学生的体育成绩分为五个等级,其中A:50分;B:49-45分;C:44-40分;D:39-30分;E:29-0分.根据所分等级情况制作了如下两个不完整的统计图表:学业模拟专试体育成绩(分数段)
| 分数段 | 人数/人 | 频数 |
| A | 48 | 0.2 |
| B | m | 0.25 |
| C | 84 | 0.35 |
| D | 36 | n |
| E | 12 | 0.05 |
(1)在统计表中,m的值为60,n的值为0.15;
(2)将统计图补充完整;
(3)如果把成绩在30分以上(含30分)定为合格,那么估计该校今年1600名九年级学生中体育成绩为合格的学生人数约有多少人?

| 组别 | 分数段 | 频数 | 频率 |
| 一 | 50.5~60.5 | 16 | 0.08 |
| 二 | 60.5~70.5 | 30 | 0.15 |
| 三 | 70.5~80.5 | m | 0.25 |
| 四 | 80.5~90.5 | 80 | n |
| 五 | 90.5~100.5 | 24 | 0.12 |
(2)补全频数分布直方图;
(3)若成绩超过80分为优秀,则该校八年级学生中汉字听写能力优秀的约有多少人?
 如图,一块长为20米,宽为8米的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为56米2,两块绿地之间及周边留有宽度相等的人形通道.
如图,一块长为20米,宽为8米的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为56米2,两块绿地之间及周边留有宽度相等的人形通道.
