��Ŀ����
13����ͼ1����ƽ��ֱ������ϵ�У���֪����ABCD����������B��1��0����C��2��0����D��2��$\sqrt{3}$����˫����y=$\frac{k}{x}$��x��0������A������P�ӵ�A���������߶�AB���B�˶���ͬʱ����Q�ӵ�C���������߶�CD���D�˶�����P��Q���˶��ٶȾ�Ϊÿ��$\sqrt{3}$����λ���˶�ʱ��Ϊt�룮��1��ֱ��д����A�����꣬�����˫���ߵĽ���ʽ��
��2����M��˫������һ���㣬����P��Q��C��MΪ������ı�����ƽ���ı��Σ���ֱ��д����M�����ꣻ
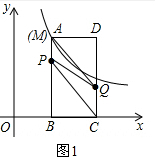
��3����ͼ2������Q��QH��CD��AC�ڵ�H���ڶ���P��Q�˶��Ĺ����У�������ƽ�����Ƿ���ڵ�N��ʹ��B��H��P��NΪ������ı���Ϊ���Σ������ڣ������t��ֵ���������ڣ���˵�����ɣ�
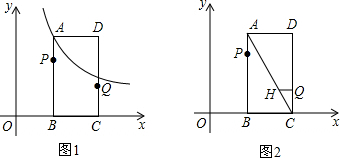
���� ��1�����ݾ��ε����ʼ��ɵõ�����
��2�����������������PQΪ�Խ���ʱ����ͼ1��PM��CQ��PM=CQ���õ�M��1��$\sqrt{3}$��������CQΪ�Խ���ʱ����ͼ2��DQ=PB��QF=FC���õ�DQ=QF=FC���������M��3��$\frac{\sqrt{3}}{3}$��������CPΪ�Խ���ʱ�������ڣ�
��3�����ڣ�����AD=1��DC=$\sqrt{3}$����á�ACD=30�㣬���ǵõ�H��2-t��$\sqrt{3}$t����p��1��$\sqrt{3}$-$\sqrt{3}$t������PH2=BH2ʱ����PH2=BH2ʱ����PB2=BH2ʱ�ֱ��з������t��ֵ��
���  �⣺��1�����ı���ABCD�Ǿ��Σ�
�⣺��1�����ı���ABCD�Ǿ��Σ�
��AB=CD��AB��x�ᣬCD��x�ᣬ
��B��1��0����D��2��$\sqrt{3}$����
��OB=1��CD=$\sqrt{3}$��
��AB=$\sqrt{3}$��
��A��1��$\sqrt{3}$����
��˫����y=$\frac{k}{x}$��x��0������A��
��k=$\sqrt{3}$��
��˫���ߵĽ���ʽΪ��y=$\frac{\sqrt{3}}{x}$��
��2���ߵ�P��Q���˶��ٶȾ�Ϊÿ��$\sqrt{3}$����λ��
�൱��PQΪ�Խ���ʱ����ͼ1��
PM��CQ��PM=CQ��
��M��A�غϣ�
��M��1��$\sqrt{3}$����
����CQΪ�Խ���ʱ����ͼ2��DQ=PB��QF=FC��
��DQ=QF=FC��
��P��1��$\frac{\sqrt{3}}{3}$����
��M��3��$\frac{\sqrt{3}}{3}$����
����CPΪ�Խ���ʱ�������ڣ�
��3�����ڣ���AD=1��DC=$\sqrt{3}$�����ACD=30�㣬B��1��0����
��H��2-t��$\sqrt{3}$t����P��1��$\sqrt{3}$-$\sqrt{3}$t����
����ƽ���ڣ���ֻҪ�ڱ���ȼ��ɣ�
��PH2=BH2ʱ������2-t-1��2+��2$\sqrt{3}$t-$\sqrt{3}$��2=��t-1��2+��$\sqrt{3}$-$\sqrt{3}$t��2��
��ã�t=0��t=$\frac{2}{3}$��
��0��t��1��
����ڣ�
��PH2=PB2ʱ����1-2+t��2+��$\sqrt{3}$-$\sqrt{3}$t-$\sqrt{3}$t��2=��$\sqrt{3}$-$\sqrt{3}$t��2��
��ã�t=$\frac{4��\sqrt{6}}{10}$����0��t��1��
��t=$\frac{4��\sqrt{6}}{10}$��
�ߵ�PB2=BH2ʱ����$\sqrt{3}$-$\sqrt{3}$t��2=��1-2+t��2+��$\sqrt{3}$t��2��
��ã�t=-2��$\sqrt{6}$��
��0��t��1��
��t=-2+$\sqrt{6}$��
������������t=0��$\frac{2}{3}$��$\frac{4��\sqrt{6}}{10}$��-2$+\sqrt{6}$ʱ����B��H��P��NΪ������ı���Ϊ���Σ�
���� ���⿼���˷��������������ʣ������Ľ���ʽ��ƽ���ı��ε��ж������ʣ����ε��ж������ʣ������������ε����ʶ����ǽ���Ĺؼ���

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д���1��ij������2�·��õ�90�ȣ������˹涨��a�ȣ�������Ӧ�ý���Ѷ���Ԫ���ú�a�Ĵ���ʽ��ʾ������90-a����0.5��
��2��ͼ�����⻧����3�¡�4�µ��õ�����ͽ��������
| �·� | �õ��� | ��������� |
| 3�� | 80�� | 25Ԫ |
| 4�� | 45�� | 10Ԫ |
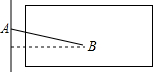 ��ͼ��������Զ����ʱ��С���ӵ�A��������ɳ����B������Զ�ɼ���4.6�ף���С���������㵽��ŵ�ľ������4.6�ף�������ڡ���С�ڡ����ڡ���
��ͼ��������Զ����ʱ��С���ӵ�A��������ɳ����B������Զ�ɼ���4.6�ף���С���������㵽��ŵ�ľ������4.6�ף�������ڡ���С�ڡ����ڡ��� ���������⣺����ͼ����ֱ֪��b��c��ֱ��a���أ�����1+��2=180�㣬��b��c���������õķ����У��ƶ�b��c��������ͬλ����ȣ���ֱ��ƽ�У�
���������⣺����ͼ����ֱ֪��b��c��ֱ��a���أ�����1+��2=180�㣬��b��c���������õķ����У��ƶ�b��c��������ͬλ����ȣ���ֱ��ƽ�У�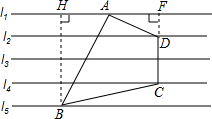 ��ͼ����ֱ֪��l1��l2��l3��l4��l5����������ƽ��ֱ��ľ��������Ϊ1������ı���ABCD���ĸ�������ƽ��ֱ���ϣ���BAD=90����AB=2AD��DC��l4��
��ͼ����ֱ֪��l1��l2��l3��l4��l5����������ƽ��ֱ��ľ��������Ϊ1������ı���ABCD���ĸ�������ƽ��ֱ���ϣ���BAD=90����AB=2AD��DC��l4�� ��������״��ȫ��ͬ���������һ���������Σ�ֻ���̶ȵ�ֱ�߰�����Ҫ��ͼ��
��������״��ȫ��ͬ���������һ���������Σ�ֻ���̶ȵ�ֱ�߰�����Ҫ��ͼ��
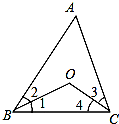 ��ͼ��BO��CO�ֱ�ƽ�֡�ABC�͡�ACB��
��ͼ��BO��CO�ֱ�ƽ�֡�ABC�͡�ACB��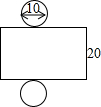 ��ͼ��ij��װ�еı���չ��ͼ��
��ͼ��ij��װ�еı���չ��ͼ��