题目内容
5.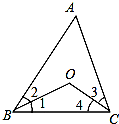 如图,BO、CO分别平分∠ABC和∠ACB.
如图,BO、CO分别平分∠ABC和∠ACB.(1)若∠A=60°,求∠O?
(2)若∠A=100°,∠O又是多少?
(3)由(1)、(2)你发现了∠O与∠A有何数量关系?(提示:三角形的内角和等于180°)
分析 已知∠A,就可以求出∠ABC与∠ACB的和,进而可以求出∠1与∠4的和.在△OBC中利用三角形内角和定理就可以求出∠BOC的大小.
解答 解:∵BO、CO分别平分∠ABC和∠ACB,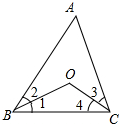
∴∠1=∠2,∠3=∠4.
(1)∵∠A=60°,
∴∠1+∠2+∠3+∠4=120°,
∴∠1+∠4=60°,
∴∠O=120°.
(2)若∠A=100°,
∴∠1+∠2+∠3+∠4=80°,
∴∠1+∠4=40°,
∴∠O=140°.
(3)数量关系是∠O=90°+$\frac{1}{2}$∠A.
点评 本题考查了三角形内角和定理.第一,第二问是解决第三问发现规律的基础,因而总结前两问中的基本解题思路是解题的关键.

练习册系列答案
相关题目
20.已知A、B在数轴上分别表示数a,b.
(1)对照数轴填写表格:
(2)试用含a,b的式子表示A、B两点间的距离;
(3)你能说明|3+6|在数轴上表示的意义吗?
(4)若点P表示的数为x,当点P在数轴上什么位置时,|x+3|+|x-4|的值最小?最小值是多少?
(1)对照数轴填写表格:
| a | 2 | -2 | 0 | -2 |
| b | 3 | 3 | 3 | -3 |
| A、B两点间的距离 |
(3)你能说明|3+6|在数轴上表示的意义吗?
(4)若点P表示的数为x,当点P在数轴上什么位置时,|x+3|+|x-4|的值最小?最小值是多少?
20.一组数据的最大值为100,最小值为61,若组距为6,则这组数据可分成( )
| A. | 5组 | B. | 6组 | C. | 7组 | D. | 8组 |
10.下列说法中正确的是( )
| A. | 一个角的补角一定比这个角大 | B. | 一个角的补角一定是钝角 | ||
| C. | 一个直角的补角是直角 | D. | 一个锐角和一个钝角一定互为补角 |
 矩形ABCD的对角线AC、BD交于点O,∠AOD=120°,AC=4,则△ABO的周长为6.
矩形ABCD的对角线AC、BD交于点O,∠AOD=120°,AC=4,则△ABO的周长为6.
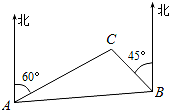 如图,C岛在A岛的北偏东60°方向,在B岛的北偏西45°方向,则∠ACB=105°.
如图,C岛在A岛的北偏东60°方向,在B岛的北偏西45°方向,则∠ACB=105°.