题目内容
1.已知⊙O的直径CD为5cm,AB是⊙O的弦,AB⊥CD,垂足为M,且AB=4,则AC=2$\sqrt{5}$或$\sqrt{5}$.分析 先画图,分两种情况:①AC>AD,如图1,连接OA,根据垂径定理得出AM,再由勾股定理得出AC;②AC<AD,如图2,连接OA,根据垂径定理得出AM,再由勾股定理得出OM,即可得出AC.
解答 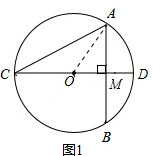 解:分两种情况:①AC>AD,如图1,连接OA,
解:分两种情况:①AC>AD,如图1,连接OA,
∵CD=5,∴OA=OC=2.5,
∵AB⊥CD,∴AM=BM,
∵AB=4,∴AM=2,
∴OM=1.5,
∴CM=4,
∴由勾股定理得AC=2$\sqrt{5}$;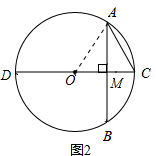
②AC<AD,如图2,连接OA,
∵CD=5,∴OA=OC=2.5,
∵AB⊥CD,∴AM=BM,
∵AB=4,∴AM=2,
∴OM=1.5,
∴CM=1,
∴由勾股定理得AC=$\sqrt{5}$;
故答案为2$\sqrt{5}$或$\sqrt{5}$.
点评 本题考查了垂径定理,以及勾股定理,分类讨论是解题的关键.

练习册系列答案
相关题目
9.已知$m=\sqrt{2}+1$,$n=\sqrt{2}-1$,则$\sqrt{{m^2}+{n^2}-3mn}$=( )
| A. | 9 | B. | $\sqrt{3}$ | C. | 3 | D. | 5 |
 如图,一次函数y=$\frac{1}{2}$x+5的图象与反比例函数y=-$\frac{k}{x}$(k为常数,且k≠0)的图象交于A(-2,b),B两点.
如图,一次函数y=$\frac{1}{2}$x+5的图象与反比例函数y=-$\frac{k}{x}$(k为常数,且k≠0)的图象交于A(-2,b),B两点.
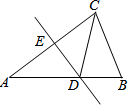 如图,在△ABC中,∠ACB=105°,AC边上的垂直平分线交AB边于点D,交AC边于点E,连结CD.
如图,在△ABC中,∠ACB=105°,AC边上的垂直平分线交AB边于点D,交AC边于点E,连结CD. 在Rt△ABC中,∠C=90°.
在Rt△ABC中,∠C=90°.