题目内容
16.已知关于x,y的方程组$\left\{\begin{array}{l}x-2y=m\\ 2x+3y=2m+4\end{array}\right.$的解满足不等式组$\left\{\begin{array}{l}3x+y≤0\\ x+5y>0\end{array}\right.$,求满足条件的m的整数值.分析 首先将两方程相加得出3x+y=3m+4,两方程相减得x+5y=m+4,代入等式组$\left\{\begin{array}{l}3x+y≤0\\ x+5y>0\end{array}\right.$中得:$\left\{\begin{array}{l}{3m+4≤0}\\{m+4>0}\end{array}\right.$,再解不等式组,确定出整数解即可.
解答 解:解方程组$\left\{\begin{array}{l}{x-2y=m}&{①}\\{2x+3y=2m+4}&{②}\end{array}\right.$,
①+②,得:3x+y=3m+4,
②-①,得:x+5y=m+4,
由$\left\{\begin{array}{l}{3x+y≤0}\\{x+5y>0}\end{array}\right.$得:$\left\{\begin{array}{l}{3m+4≤0}\\{m+4>0}\end{array}\right.$,
解不等式组得:-4<m≤-$\frac{4}{3}$,
则m=-3或m=-2.
点评 此题主要考查了一元一次不等式组的整数解,以及二元一次方程的解,关键是掌握消元的方法,用含m的式子表示x、y.

练习册系列答案
 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
6.计算-(-1)2014的结果是( )
| A. | 2014 | B. | -2014 | C. | 1 | D. | -1 |
4.以下元素对应相等,不能判定两个三角形全等的是( )
| A. | 三个角 | B. | 两边及夹角 | C. | 两角和一边 | D. | 三条边 |
5.设函数y=x2+2kx+k-1(k为常数),下列说法正确的是( )
| A. | 对任意实数k,函数与x轴都没有交点 | |
| B. | 存在实数n,满足当x≥n时,函数y的值都随x的增大而减小 | |
| C. | k取不同的值时,二次函数y的顶点始终在同一条直线上 | |
| D. | 对任意实数k,抛物线y=x2+2kx+k-1都必定经过唯一定点 |
 已知?ABCD中,点E,F分别是AD,CB延长线上的点,且∠1=∠2,DF交AB于点G,BE交CD于点H,求证:EH=FG.
已知?ABCD中,点E,F分别是AD,CB延长线上的点,且∠1=∠2,DF交AB于点G,BE交CD于点H,求证:EH=FG.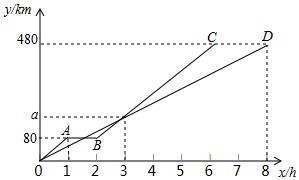 甲、乙两地相距480km,客车、货车同时从甲地出发去乙地,贷车匀速行驶,客车途中停车检修1h,然后提高速度匀速行驶.图中折线OA-AB-BC、线段OD分别表示客车、货车所行驶路程y km与时间x h之间的函数图象.
甲、乙两地相距480km,客车、货车同时从甲地出发去乙地,贷车匀速行驶,客车途中停车检修1h,然后提高速度匀速行驶.图中折线OA-AB-BC、线段OD分别表示客车、货车所行驶路程y km与时间x h之间的函数图象.