题目内容
20.下列等式成立的是( )| A. | $\frac{2}{2x+y}=\frac{1}{x+y}$ | B. | (-x-1)(1-x)=1-x2 | C. | $\frac{x}{-x+y}=-\frac{x}{x+y}$ | D. | (-x-1)2=x2+2x+1 |
分析 利用分式的性质以及整式混合运算的计算方法逐一计算结果,进一步判断得出答案即可.
解答 解:A、$\frac{2}{2x+y}$不能约分,此选项错误;
B、(-x-1)(1-x)=-1+x2,此选项错误;
C、$\frac{x}{-x+y}$=-$\frac{x}{x-y}$,此选项错误;
D、(-x-1)2=x2+2x+1,此选项正确.
故选:D.
点评 此题考查分式的混合运算,整式的混合运算,掌握分式的性质和整式混合运算的方法是解决问题的关键.

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
10.小明有两根3cm、7cm的木棒,他想以这两根木棒为边做一个三角形,还需再选用的木棒长可以为( )
| A. | 3cm | B. | 4cm | C. | 9cm | D. | 10cm |
5.设函数y=x2+2kx+k-1(k为常数),下列说法正确的是( )
| A. | 对任意实数k,函数与x轴都没有交点 | |
| B. | 存在实数n,满足当x≥n时,函数y的值都随x的增大而减小 | |
| C. | k取不同的值时,二次函数y的顶点始终在同一条直线上 | |
| D. | 对任意实数k,抛物线y=x2+2kx+k-1都必定经过唯一定点 |
 已知?ABCD中,点E,F分别是AD,CB延长线上的点,且∠1=∠2,DF交AB于点G,BE交CD于点H,求证:EH=FG.
已知?ABCD中,点E,F分别是AD,CB延长线上的点,且∠1=∠2,DF交AB于点G,BE交CD于点H,求证:EH=FG.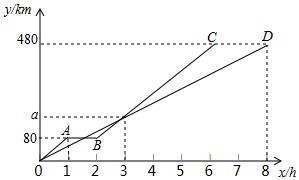 甲、乙两地相距480km,客车、货车同时从甲地出发去乙地,贷车匀速行驶,客车途中停车检修1h,然后提高速度匀速行驶.图中折线OA-AB-BC、线段OD分别表示客车、货车所行驶路程y km与时间x h之间的函数图象.
甲、乙两地相距480km,客车、货车同时从甲地出发去乙地,贷车匀速行驶,客车途中停车检修1h,然后提高速度匀速行驶.图中折线OA-AB-BC、线段OD分别表示客车、货车所行驶路程y km与时间x h之间的函数图象.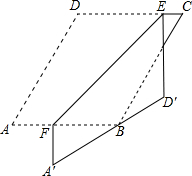 如图,在?ABCD纸片中,∠A=60°,AD-AB=1,点E,F分别在边CD,AB上,将纸片沿EF折叠,使点A,D分别落在点A′,D′,处,且AD经过点B.当D′E⊥CD时,CE=1,则AB的长是$\frac{3\sqrt{3}+5}{2}$.
如图,在?ABCD纸片中,∠A=60°,AD-AB=1,点E,F分别在边CD,AB上,将纸片沿EF折叠,使点A,D分别落在点A′,D′,处,且AD经过点B.当D′E⊥CD时,CE=1,则AB的长是$\frac{3\sqrt{3}+5}{2}$.