题目内容
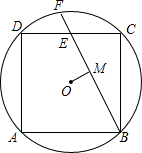 如图,正方形ABCD内接于⊙O,E为DC的中点,直线BE交⊙O于点F,如果⊙O的半径为2
如图,正方形ABCD内接于⊙O,E为DC的中点,直线BE交⊙O于点F,如果⊙O的半径为2| 2 |
考点:正多边形和圆
专题:
分析:连接OA、OB、OD,求出AD,求出CE,根据勾股定理求出BE,根据相交弦定理求出EF,根据垂径定理求出BM,在△BOM中,根据勾股定理求出OM即可.
解答: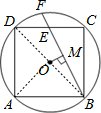 解:连接OD,OA,OB,
解:连接OD,OA,OB,
∵正方形ABCD内接于⊙O,
∴∠AOD=
×360°=90°,
在△AOD中,由勾股定理得:AD=
=
=4,
∴CD=AD=BC=4,
∵E是CD中点,
∴DE=CE=2,
在△BCE中由勾股定理得:BE=
=2
,
由相交弦定理得:CE×DE=BE×EF,
即2×2=2
EF,
∴EF=
,
∴BF=2
+
=
,
∵OM⊥BF,OM过圆心O,
∴BM=FM=
BF=
,
在△BOM中,由勾股定理得:OB2=OM2+BM2,
即(2
)2=OM2+(
)2,
解得:OM=
.
故答案为
.
 解:连接OD,OA,OB,
解:连接OD,OA,OB,∵正方形ABCD内接于⊙O,
∴∠AOD=
| 1 |
| 4 |
在△AOD中,由勾股定理得:AD=
| OD2+OA2 |
(2
|
∴CD=AD=BC=4,
∵E是CD中点,
∴DE=CE=2,
在△BCE中由勾股定理得:BE=
| 22+42 |
| 5 |
由相交弦定理得:CE×DE=BE×EF,
即2×2=2
| 5 |
∴EF=
2
| ||
| 5 |
∴BF=2
| 5 |
2
| ||
| 5 |
12
| ||
| 5 |
∵OM⊥BF,OM过圆心O,
∴BM=FM=
| 1 |
| 2 |
6
| ||
| 5 |
在△BOM中,由勾股定理得:OB2=OM2+BM2,
即(2
| 2 |
6
| ||
| 5 |
解得:OM=
2
| ||
| 5 |
故答案为
2
| ||
| 5 |
点评:本题考查了正多边形和圆,综合运用了垂径定理,勾股定理,相交弦定理,正方形的性质等知识点,关键是构造直角三角形,并进一步求出BM长,主要培养了学生运用定理进行推理和计算的能力,题型较好,具有一定的代表性,难度适中.

练习册系列答案
相关题目
在圆内接正十边形中,AB是正十边形的一条边,圆的半径为2,则圆内接正十边形的边长AB为( )
A、3-
| ||||
B、
| ||||
C、
| ||||
D、
|
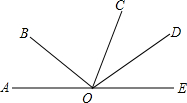 如图,点A、O、E在同一条直线上,∠AOB=40°,∠DOB=105°,OD平分∠COE.
如图,点A、O、E在同一条直线上,∠AOB=40°,∠DOB=105°,OD平分∠COE. 如图,E为边长为2的正方形ABCD的对角线BD上的一点,且BE=BC,P为CE上任意一点,PQ⊥BC于点Q,PR⊥BE于点R,则PQ+PR的值是
如图,E为边长为2的正方形ABCD的对角线BD上的一点,且BE=BC,P为CE上任意一点,PQ⊥BC于点Q,PR⊥BE于点R,则PQ+PR的值是 如图,函数y1=-x+4的图象与函数y2=
如图,函数y1=-x+4的图象与函数y2= 如图,已知点G是梯形ABCD的中位线EF上任意一点,若梯形ABCD的面积为28cm2,则图中阴影部分的面积为
如图,已知点G是梯形ABCD的中位线EF上任意一点,若梯形ABCD的面积为28cm2,则图中阴影部分的面积为