题目内容
 如图,已知点G是梯形ABCD的中位线EF上任意一点,若梯形ABCD的面积为28cm2,则图中阴影部分的面积为
如图,已知点G是梯形ABCD的中位线EF上任意一点,若梯形ABCD的面积为28cm2,则图中阴影部分的面积为考点:梯形中位线定理
专题:
分析:设三角形EGA的EG边上的高为a,三角形GFC的GF边上的高为a,则梯形的高为2a,利用中位线的性质及梯形的面积求得阴影部分的面积的和即可.
解答:解:设三角形EGA的EG边上的高为a,则三角形GFC的GF边上的高为a,则梯形的高为2a,
∵点G是梯形ABCD的中位线EF上任意一点,
∴S阴影部分=S△EGA+S△GFC=
×EG×a+
GF×a=
EF×a
∵EF=
(AD+BC)
∴
a•EF=
a×
(AD+BC)=
a(AD+BC)
∵S梯形=
(AD+BC)•2a=(AD+BC)•a
∴S阴影部分=
a•EF=
a(AD+BC)=
S梯形=
×28=7,
故答案为7.
∵点G是梯形ABCD的中位线EF上任意一点,
∴S阴影部分=S△EGA+S△GFC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵EF=
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
∵S梯形=
| 1 |
| 2 |
∴S阴影部分=
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
故答案为7.
点评:本题考查了梯形的中位线定理,正确的利用梯形的中位线定理是解决此类问题的关键.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
 如图,小红作出了边长为1的第1个正△A1B1C1,算出了正△A1B1C1的面积,然后分别取△A1B1C1三边的中点A2,B2,C2,作出了第2个正△A2B2C2,算出了正△A2B2C2的面积,用同样的方法,作出了第3个正△A3B3C3,算出了正△A3B3C3的面积…,由此可得,第8个正△A8B8C8的面积是( )
如图,小红作出了边长为1的第1个正△A1B1C1,算出了正△A1B1C1的面积,然后分别取△A1B1C1三边的中点A2,B2,C2,作出了第2个正△A2B2C2,算出了正△A2B2C2的面积,用同样的方法,作出了第3个正△A3B3C3,算出了正△A3B3C3的面积…,由此可得,第8个正△A8B8C8的面积是( )A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
若方程组
无解,则( )
|
| A、a,b可取任意常数 |
| B、a=-6,b可取任意常数 |
| C、a可取任意常数,b≠200 |
| D、a=-6,且b≠200 |
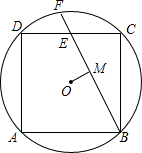 如图,正方形ABCD内接于⊙O,E为DC的中点,直线BE交⊙O于点F,如果⊙O的半径为2
如图,正方形ABCD内接于⊙O,E为DC的中点,直线BE交⊙O于点F,如果⊙O的半径为2 如图,直线y=k1x+b与反比例函数y=
如图,直线y=k1x+b与反比例函数y=