题目内容
 如图,E为边长为2的正方形ABCD的对角线BD上的一点,且BE=BC,P为CE上任意一点,PQ⊥BC于点Q,PR⊥BE于点R,则PQ+PR的值是
如图,E为边长为2的正方形ABCD的对角线BD上的一点,且BE=BC,P为CE上任意一点,PQ⊥BC于点Q,PR⊥BE于点R,则PQ+PR的值是考点:正方形的性质
专题:
分析:连接BP,设点C到BE的距离为h,然后根据S△BCE=S△BCP+S△BEP求出h=PQ+PR,再根据正方形的性质求出h即可.
解答: 解:如图,连接BP,设点C到BE的距离为h,
解:如图,连接BP,设点C到BE的距离为h,
则S△BCE=S△BCP+S△BEP,
即
BE•h=
BC•PQ+
BE•PR,
∵BE=BC,
∴h=PQ+PR,
∵正方形ABCD的边长为2,
∴h=2×
=
.
故答案为:
.
 解:如图,连接BP,设点C到BE的距离为h,
解:如图,连接BP,设点C到BE的距离为h,则S△BCE=S△BCP+S△BEP,
即
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵BE=BC,
∴h=PQ+PR,
∵正方形ABCD的边长为2,
∴h=2×
| ||
| 2 |
| 2 |
故答案为:
| 2 |
点评:本题考查了正方形的性质,三角形的面积,熟记性质并作辅助线,利用三角形的面积求出PQ+PR等于点C到BE的距离是解题的关键.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
下列各式一定成立的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知关于x的方程
+
=
恰有一个实根,则满足条件的实数a的值的个数为( )
| x |
| x-2 |
| x-2 |
| x |
| a-x |
| x2-2x |
| A、1 | B、2 | C、3 | D、4 |
在Rt△ABC中,∠C=90°,AC=6cm,BC=8cm,则它的外心与顶点C的距离为( )
| A、5cm | B、6cm |
| C、7cm | D、8cm |
 如图,小红作出了边长为1的第1个正△A1B1C1,算出了正△A1B1C1的面积,然后分别取△A1B1C1三边的中点A2,B2,C2,作出了第2个正△A2B2C2,算出了正△A2B2C2的面积,用同样的方法,作出了第3个正△A3B3C3,算出了正△A3B3C3的面积…,由此可得,第8个正△A8B8C8的面积是( )
如图,小红作出了边长为1的第1个正△A1B1C1,算出了正△A1B1C1的面积,然后分别取△A1B1C1三边的中点A2,B2,C2,作出了第2个正△A2B2C2,算出了正△A2B2C2的面积,用同样的方法,作出了第3个正△A3B3C3,算出了正△A3B3C3的面积…,由此可得,第8个正△A8B8C8的面积是( )A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
若方程组
无解,则( )
|
| A、a,b可取任意常数 |
| B、a=-6,b可取任意常数 |
| C、a可取任意常数,b≠200 |
| D、a=-6,且b≠200 |
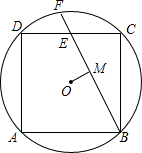 如图,正方形ABCD内接于⊙O,E为DC的中点,直线BE交⊙O于点F,如果⊙O的半径为2
如图,正方形ABCD内接于⊙O,E为DC的中点,直线BE交⊙O于点F,如果⊙O的半径为2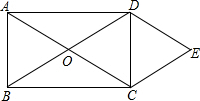 如图所示,O为矩形ABCD的对角线的交点,DE∥AC,CE∥BD.
如图所示,O为矩形ABCD的对角线的交点,DE∥AC,CE∥BD.