题目内容
1. 如图,四边形ABCD是直角梯形,∠C=90°,AO⊥BC于点O.A、B、C、D、O分别在边长为I的小正方形网格上.以O为原点,BC所在直线为x轴,建立平面直角坐标系.
如图,四边形ABCD是直角梯形,∠C=90°,AO⊥BC于点O.A、B、C、D、O分别在边长为I的小正方形网格上.以O为原点,BC所在直线为x轴,建立平面直角坐标系.(1)AB=5(直接写出);
(2)画出将△AOB饶点O逆时针旋转点90°所得到的△A1OB1,并求点A到点A1所走的路线长:
(3)求∠ABD的正切值.
分析 (1)由题意可知,△OAB是直角三角形,有勾股定理求AB的长;
(2)因为旋转不改变图形的大小与形状,所以找出旋转后的对应点即可;
(3)过点A作BD的垂线构造三角形后设法求∠ABD的正切值.
解答 解:(1)在Rt△AOB中,
∵AB2=OA2+OB2
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=$\sqrt{25}$=5.
(2)如下图所示: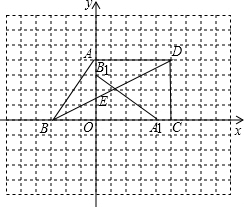
图中△A1 OB1 是将△AOB饶点O逆时针旋转点90°所得到的.
求点A到点A1所走的路线长=$\widehat{A{A}_{1}}$=$\frac{1}{4}$×2π×4=2π
(3)由图可知:
∵AB=AD=5,
∴∠ABD=∠ADB
∴tan∠ABD=tan∠ADB=$\frac{AE}{AD}$
∵四边形ABCD是直角梯形,∠C=90°,
∴AD∥BC,
∠ADB=∠DBC
tan∠ABD=$\frac{DC}{BC}$=$\frac{4}{8}$=$\frac{1}{2}$
点评 本题考查了图形的旋转、直角梯形的性质、三角函数等知识点,解题的关键是掌握旋转的性质及三角函数的定义.

练习册系列答案
相关题目
13.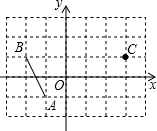 如图,在平面直角坐标系中,把线段AB进行平移,使得点A到达点C(3,1),点B到点D,则点D的坐标为( )
如图,在平面直角坐标系中,把线段AB进行平移,使得点A到达点C(3,1),点B到点D,则点D的坐标为( )
 如图,在平面直角坐标系中,把线段AB进行平移,使得点A到达点C(3,1),点B到点D,则点D的坐标为( )
如图,在平面直角坐标系中,把线段AB进行平移,使得点A到达点C(3,1),点B到点D,则点D的坐标为( )| A. | (3,2) | B. | (2,1) | C. | (1,3) | D. | (2,3) |
 如图,∠POQ=45°,画△ABC关于OP对称的△A1B1C1,再画出△A1B1C1关于OQ对称△A2B2C2,△A2B2C2能否看作由△ABC旋转而得到的?如果能,找出旋转中心和旋转角度,如果不能,请说明理由.
如图,∠POQ=45°,画△ABC关于OP对称的△A1B1C1,再画出△A1B1C1关于OQ对称△A2B2C2,△A2B2C2能否看作由△ABC旋转而得到的?如果能,找出旋转中心和旋转角度,如果不能,请说明理由.
 在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-4,5),
在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-4,5), 在平面直角坐标系中,三角形ABC的三个顶点的位置如图所示,现将三角形ABC平移,使得点A移至图中点A′的位置.(1)在平面直角坐标系中,画出平移后所得三角形A′B′C′(其中B′,C′分别是点B,C的对应点).
在平面直角坐标系中,三角形ABC的三个顶点的位置如图所示,现将三角形ABC平移,使得点A移至图中点A′的位置.(1)在平面直角坐标系中,画出平移后所得三角形A′B′C′(其中B′,C′分别是点B,C的对应点). 如图,源源想把房子向下平移3个单位长度,你能帮他办到吗?请作出相应图案,并写出平移后的A、B、C、D、E、F、G点的坐标.
如图,源源想把房子向下平移3个单位长度,你能帮他办到吗?请作出相应图案,并写出平移后的A、B、C、D、E、F、G点的坐标.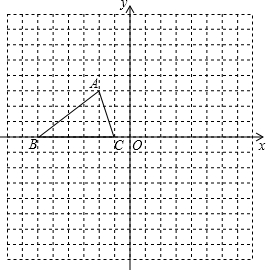 如图,已知△ABC的三个顶点的坐标分别为A(-2,3)、B(-6,0),C(-1,0).
如图,已知△ABC的三个顶点的坐标分别为A(-2,3)、B(-6,0),C(-1,0).