题目内容
两车在两城间不断往返行驶:甲车从A城开出,乙车从B城开出,且比甲车早出发1小时,两车在途中距A、B两城分别为200公里和240公里的C处相遇;相遇后乙车改为按甲车速度行驶,而甲车却提速若干公里/时,两车恰巧又在C处相遇;然后甲车再次提速5公里/时,乙车则提速50公里/时,两车恰巧又在C处相遇.那么从起行到第3次相遇,乙车共行驶了 小时.
考点:分式方程的应用
专题:
分析:可设初时甲车的速度为x公里/时,甲车先提速了y公里/时,进而根据时间的等量关系得到相应的方程列方程求解,进而得到乙车行驶时间.
解答: 解:设初时甲车速为x公里/时,甲车先提速了y公里/时,则由后2次相遇于C得:
解:设初时甲车速为x公里/时,甲车先提速了y公里/时,则由后2次相遇于C得:
,
解得
,
经检验,得
是原方程组的解.
第1次相遇于C,甲车行驶时间为:200÷100=2(小时),则乙车行驶时间为:2+1=3(小时),
第2次相遇于C,乙车行驶时间为:400÷100=4(小时),
第3次相遇于C,乙车行驶时间为:480÷150=3.2(小时),
故乙车行驶时间一共为:3+4+3.2=10.2(小时).
故答案为10.2.
 解:设初时甲车速为x公里/时,甲车先提速了y公里/时,则由后2次相遇于C得:
解:设初时甲车速为x公里/时,甲车先提速了y公里/时,则由后2次相遇于C得:
|
解得
|
经检验,得
|
第1次相遇于C,甲车行驶时间为:200÷100=2(小时),则乙车行驶时间为:2+1=3(小时),
第2次相遇于C,乙车行驶时间为:400÷100=4(小时),
第3次相遇于C,乙车行驶时间为:480÷150=3.2(小时),
故乙车行驶时间一共为:3+4+3.2=10.2(小时).
故答案为10.2.
点评:本题考查分式方程的应用;得到甲车的速度是解决本题的突破点;注意从第一次相遇到第二次相遇时甲车和乙车的行驶时间相同,从第二次相遇到第三次相遇时甲车和乙车的行驶时间也相同.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设n=100100101101102102103103…109109,则n不能被( )整除.
| A、7 | B、9 | C、11 | D、13 |
已知△ABC的三条长a、b、c满足b+c=8,bc=a2-12a+52,则△ABC的形状一定是( )
| A、等腰三角形 |
| B、直角三角形 |
| C、等腰直角三角形 |
| D、无法确定 |
小马在计算“41+x”时,误将“+”看成“-”,结果得12,则41+x的值应为( )
| A、29 | B、53 | C、67 | D、70 |
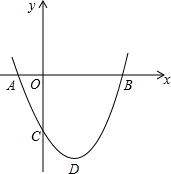 如图,二次函数y=ax2+bx+c(a>0).图象的顶点为D,其图象与x轴的交点A、B的横坐标分别为-1、3,与y轴负半轴交于点C.下面五个结论:①2a+b=0;②a+b+c>0;③当x≤1时,y随x值的增大而增大;④当-1≤x≤3时,ax2+bx+c<0;⑤只有当a=
如图,二次函数y=ax2+bx+c(a>0).图象的顶点为D,其图象与x轴的交点A、B的横坐标分别为-1、3,与y轴负半轴交于点C.下面五个结论:①2a+b=0;②a+b+c>0;③当x≤1时,y随x值的增大而增大;④当-1≤x≤3时,ax2+bx+c<0;⑤只有当a=