题目内容
6. 如图,在△ABC中,AB=AC,D为BC的中点,AE∥BC,DE∥AB.求证:四边形ADCE为矩形.
如图,在△ABC中,AB=AC,D为BC的中点,AE∥BC,DE∥AB.求证:四边形ADCE为矩形.
分析 依据“对边平行且相等”的四边形是平行四边形判定四边形ADCE是平行四边形,又由“有一内角为直角的平行四边形是矩形”证得结论.
解答 证明:∵AE∥BC,
∴AE∥BD.
又∵DE∥AB,
∴四边形ABDE是平行四边形,
∴AE=BD.
∵D为BC的中点,
∴BD=DC,
∴AE=DC;
∵AE∥CD,AE=BD=DC,即AE=DC,
∴四边形ADCE是平行四边形.
又∵AB=AC,D为BC的中点,
∴AD⊥CD,
∴平行四边形ADCE为矩形.
点评 本题考查了等腰三角形的性质、矩形的判定与性质、平行四边形的性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
14.下列事件中,是不可能事件的是( )
| A. | 抛掷2枚正方体骰子,都是6点朝上 | |
| B. | 抛掷2枚硬币,朝上的都是反面 | |
| C. | 从只装有红球的袋子中摸出白球 | |
| D. | 从只装有红、篮球的袋子中摸出篮球 |
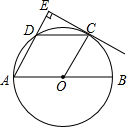 如图,AB是⊙O的直径,点C、D为半圆O的三等分点,过点C作CE⊥AD,交AD的延长线于点E.
如图,AB是⊙O的直径,点C、D为半圆O的三等分点,过点C作CE⊥AD,交AD的延长线于点E. 如图,在△ABC中,AB=7cm,AC=4cm,BC的垂直平分线分别交AB、BC于D、E,则△ACD的周长为11cm.
如图,在△ABC中,AB=7cm,AC=4cm,BC的垂直平分线分别交AB、BC于D、E,则△ACD的周长为11cm. 如图,一长度为10的线段AC的两个端点A、C分别在y轴和x轴的正半轴上滑动,以A为直角顶点,AC为直角边在第一象限内作等腰直角△ABC,连接BO.
如图,一长度为10的线段AC的两个端点A、C分别在y轴和x轴的正半轴上滑动,以A为直角顶点,AC为直角边在第一象限内作等腰直角△ABC,连接BO.



