题目内容
19.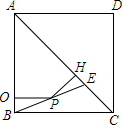 如图,正方形ABCD中,AC=2$\sqrt{2}$,对角线AC上点E,且AE=AD,连接BE,P为BE上的动点(与B,E不重合),过P作PO⊥AB,PH⊥AC分别交AB,AC于点O,H,则PO+PH的值等于( )
如图,正方形ABCD中,AC=2$\sqrt{2}$,对角线AC上点E,且AE=AD,连接BE,P为BE上的动点(与B,E不重合),过P作PO⊥AB,PH⊥AC分别交AB,AC于点O,H,则PO+PH的值等于( )| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
分析 作BM⊥AC于M,连接AP,由正方形的性质得出BM=AM=CN=$\frac{1}{2}$AC=$\sqrt{2}$,由△ABE的面积=△ABP的面积+△AEP的面积,得出AE(PO+PH)=AE•BM,得出PO+PH=BM=$\sqrt{2}$即可.
解答 解:作BM⊥AC于M,连接AP,如图所示: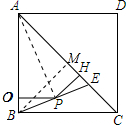
四边形ABCD是正方形,
∴AB=BC=AD,∠ABC=90°,∠BAC=45°,
∵BM⊥AC,
∴BM=AM=CN=$\frac{1}{2}$AC=$\sqrt{2}$,
∵AE=AD,
∴AE=AB,
∵△ABE的面积=△ABP的面积+△AEP的面积=$\frac{1}{2}$AB•PO+$\frac{1}{2}$AE•PH=$\frac{1}{2}$AE•BM,
∴AE(PO+PH)=AE•BM,
∴PO+PH=BM=$\sqrt{2}$;
故选:B.
点评 本题考查了正方形的性质、等腰直角三角形的性质、三角形面积的计算;熟练掌握正方形的性质,由三角形面积的计算方法得出结果是解决问题的关键.

练习册系列答案
相关题目
10.某厂一周计划生产700个零件,平均每天生产100个,由于各种原因实际每天生产量与计划量相比有出入,如表是某周每天的生产情况(超产为正,减产为负.单位:个)
该厂实行计件工资制,每生产一个零件10元,若当天超额完成任务,当天超出部分每个15元,若当天完不成任务当天生产出的零件每个只能按5元发工资,那么该厂工人这一周的工资总额是多少?
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减 | +2 | -3 | -1 | +8 | -7 | +10 | -5 |
9.下列函数中,是二次函数的是( )
| A. | y=$\frac{1}{2}$x | B. | y=x2+1 | C. | y=$\frac{2}{x-3}$ | D. | y=-$\frac{3}{x}$ |
 如图,△ABC中,DE是AC的垂直平分线,△BCD和△ABC的周长分别为14和22,则AE长为4.
如图,△ABC中,DE是AC的垂直平分线,△BCD和△ABC的周长分别为14和22,则AE长为4.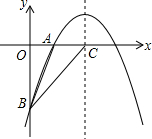 如图,二次函数y=$\frac{1}{2}$x2+bx+c的图象经过A (2,0),B(0,-6)两点.求这个二次函数的解析式.
如图,二次函数y=$\frac{1}{2}$x2+bx+c的图象经过A (2,0),B(0,-6)两点.求这个二次函数的解析式.
 如图,在l上找一点P,使|PA-PB|最大.
如图,在l上找一点P,使|PA-PB|最大.