题目内容
9．
如图，△ABC中，DE是AC的垂直平分线，△BCD和△ABC的周长分别为14和22，则AE长为4．
分析 根据线段的垂直平分线的性质得到DA=DC，根据三角形的周长公式计算即可．
解答 解：∵DE是AC的垂直平分线，
∴DA=DC，
由题意得，BD+DC+BC=14，AB+BC+AC=22，
则AC=8，
∵DE是AC的垂直平分线，
∴AE=4，
故答案为：4．
点评 本题考查的是线段的垂直平分线的性质，掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键．
练习册系列答案
相关题目
20．比1小5的数是（ ）
| A． | -4 | B． | 6 | C． | -6 | D． | 4 |
17．下列几何图形不是轴对称图形的是（ ）
| A． | 线段 | B． | 角 | C． | 平行四边形 | D． | 等腰三角形 |
1．将一个正方体的表面沿某些棱展开，能展开成的平面图形为（ ）
| A． |  | B． |  | C． |  | D． |  |
18．在直角坐标系中，点A、B的坐标分别为（1，4）和（3，0），点C是y轴上的一个动点，且A、B、C三点不在同一直线上，当△ABC的周长最小时，点C的坐标可能是（ ）
| A． | （0，0） | B． | （0，-1） | C． | （0，5） | D． | （0，3） |
19．
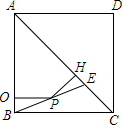如图，正方形ABCD中，AC=2$\sqrt{2}$，对角线AC上点E，且AE=AD，连接BE，P为BE上的动点（与B，E不重合），过P作PO⊥AB，PH⊥AC分别交AB，AC于点O，H，则PO+PH的值等于（ ）
如图，正方形ABCD中，AC=2$\sqrt{2}$，对角线AC上点E，且AE=AD，连接BE，P为BE上的动点（与B，E不重合），过P作PO⊥AB，PH⊥AC分别交AB，AC于点O，H，则PO+PH的值等于（ ）| A． | 1 | B． | $\sqrt{2}$ | C． | $\sqrt{3}$ | D． | 2 |