题目内容
14．若一元二次方程x2-x+k=0有实数根，求k的取值范围．分析 根据△的意义得到△=（-1）2-4k≥0，然后解不等式即可．
解答 解：∵一元二次方程x2-x+k=0有实数根，
∴△=（-1）2-4k≥0，
∴k≤$\frac{1}{4}$．
点评 本题考查了一元二次方程ax2+bx+c=0（a≠0）的根的判别式△=b2-4ac：当△＞0，方程有两个不相等的实数根；当△=0，方程有两个相等的实数根；当△＜0，方程没有实数根．
练习册系列答案
相关题目
5．用平面去截五棱柱，在所得的截面中，不可能出现的是（ ）
| A． | 八边形 | B． | 四边形 | C． | 六边形 | D． | 三角形 |
2．要组织一次排球邀请赛，参赛的每两个队之间都要比赛一场，赛程计划安排4天，每天安排7场比赛．设比赛组织者应邀请x个队参赛，则x满足的关系式为（ ）
| A． | $\frac{1}{2}$x（x+1）=28 | B． | $\frac{1}{2}$x（x-1）=28 | C． | x（x+1）=28 | D． | x（x-1）=28 |
19．
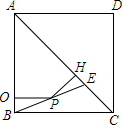如图，正方形ABCD中，AC=2$\sqrt{2}$，对角线AC上点E，且AE=AD，连接BE，P为BE上的动点（与B，E不重合），过P作PO⊥AB，PH⊥AC分别交AB，AC于点O，H，则PO+PH的值等于（ ）
如图，正方形ABCD中，AC=2$\sqrt{2}$，对角线AC上点E，且AE=AD，连接BE，P为BE上的动点（与B，E不重合），过P作PO⊥AB，PH⊥AC分别交AB，AC于点O，H，则PO+PH的值等于（ ）| A． | 1 | B． | $\sqrt{2}$ | C． | $\sqrt{3}$ | D． | 2 |
