题目内容
7.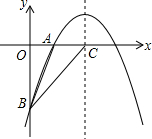 如图,二次函数y=$\frac{1}{2}$x2+bx+c的图象经过A (2,0),B(0,-6)两点.求这个二次函数的解析式.
如图,二次函数y=$\frac{1}{2}$x2+bx+c的图象经过A (2,0),B(0,-6)两点.求这个二次函数的解析式.
分析 直接把A点和B点坐标代入解析式得到关于b和c的方程组,然后解方程组确定b和c的值,从而得到二次函数解析式.
解答 解:把A (2,0),B(0,-6)的坐标分别代入y=$\frac{1}{2}$x2+bx+c中得,
$\left\{\begin{array}{l}{\frac{1}{2}×4+2b+c=0}\\{c=-6}\end{array}\right.$,
解得$\left\{\begin{array}{l}{b=2}\\{c=-6}\end{array}\right.$,
故这个二次函数的解析式为y=$\frac{1}{2}$x2+2x-6.
点评 本题考查了用待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.

练习册系列答案
相关题目
17.下列几何图形不是轴对称图形的是( )
| A. | 线段 | B. | 角 | C. | 平行四边形 | D. | 等腰三角形 |
18.在直角坐标系中,点A、B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,且A、B、C三点不在同一直线上,当△ABC的周长最小时,点C的坐标可能是( )
| A. | (0,0) | B. | (0,-1) | C. | (0,5) | D. | (0,3) |
15.下列汉字是轴对称图形的是( )
| A. | 王 | B. | 国 | C. | 洋 | D. | 告 |
2.要组织一次排球邀请赛,参赛的每两个队之间都要比赛一场,赛程计划安排4天,每天安排7场比赛.设比赛组织者应邀请x个队参赛,则x满足的关系式为( )
| A. | $\frac{1}{2}$x(x+1)=28 | B. | $\frac{1}{2}$x(x-1)=28 | C. | x(x+1)=28 | D. | x(x-1)=28 |
19.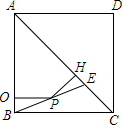 如图,正方形ABCD中,AC=2$\sqrt{2}$,对角线AC上点E,且AE=AD,连接BE,P为BE上的动点(与B,E不重合),过P作PO⊥AB,PH⊥AC分别交AB,AC于点O,H,则PO+PH的值等于( )
如图,正方形ABCD中,AC=2$\sqrt{2}$,对角线AC上点E,且AE=AD,连接BE,P为BE上的动点(与B,E不重合),过P作PO⊥AB,PH⊥AC分别交AB,AC于点O,H,则PO+PH的值等于( )
 如图,正方形ABCD中,AC=2$\sqrt{2}$,对角线AC上点E,且AE=AD,连接BE,P为BE上的动点(与B,E不重合),过P作PO⊥AB,PH⊥AC分别交AB,AC于点O,H,则PO+PH的值等于( )
如图,正方形ABCD中,AC=2$\sqrt{2}$,对角线AC上点E,且AE=AD,连接BE,P为BE上的动点(与B,E不重合),过P作PO⊥AB,PH⊥AC分别交AB,AC于点O,H,则PO+PH的值等于( )| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
17.下列代数式:a,-ab,m+n,x2+y2,-1,$\frac{1}{2}$ab2c,其中单项式共有( )
| A. | 6个 | B. | 5个 | C. | 4个 | D. | 3个 |
 制作圆弧形弯管时,需要先按中心线计算“展直长度”再下料,如图,测得弯管中心线A的半径为90cm,线段AB长为138cm,求弯管中心线$\widehat{AB}$的长(精确到1cm).
制作圆弧形弯管时,需要先按中心线计算“展直长度”再下料,如图,测得弯管中心线A的半径为90cm,线段AB长为138cm,求弯管中心线$\widehat{AB}$的长(精确到1cm).