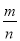题目内容
某人在做掷硬币试验时,投掷m次,正面朝上有n次
,则下列说法中正确的是( )
A. P一定等于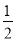
B. P一定不等于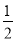
C. 多投一次,P更接近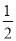
D. 随投掷次数逐渐增加,P在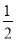
附近摆动
D
【解析】利用频率估计概率时，只有大量试验，才能用频率估计概率。因为硬币只有正反两面，所以投掷时正面朝上的概率为。因此随着投掷次数逐渐增加，稳定在附近.
故选D.
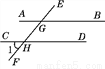
如图，AB∥CD，EF分别交AB，CD于G，H两点，若∠1＝50°，则∠EGB＝________．
某商场设立了一个可以自由转动的转盘,并规定:顾客购物10元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品(如图所示).下表是活动进行中的一组统计数据:
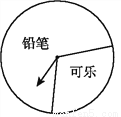
转动转盘 的次数n | 100 | 150 | 200 | 500 | 800 | 1 000 |
落在“铅笔” 区域的次数m | 68 | 111 | 136 | 345 | 564 | 701 |
落在“铅笔” 区域的频率 |
(1)计算并完成表格.
(2)请估计,当n很大时,落在“铅笔”区域的频率将会接近多少?
(3)假如你去转动该转盘一次,你获得哪种奖品的机会大?
(4)在该转盘中,表示“铅笔”区域的扇形的圆心角约是多少?
（1）0.68，0.74，0.68，0.69，0.705，0.701；（2）0.7；（3）铅笔；（4）252°.
【解析】分析：（1）根据频率的算法：频率=频数总数可得各个频率，据此填空即可；
（2）、（3）根据频率的定义，可得当n很大时，频率将会接近其概率进行解答；
（4）根据扇形图中，每部分占总体的百分比等于该部分所对应的扇形圆心角的度数与360°的比计算即可.
本题解... 小胡将一枚质地均匀的硬币抛掷了10次,正面朝上的情况出现了6次,若用A表示正面朝上这一事件,则事件A发生的( )
A. 频率是0.4 B. 频率是0.6
C. 频率是6 D. 频率接近0.6
B
【解析】总共抛10次硬币，正面朝上的次数为6次，那么正面朝上的概率是，即0.6，而频率则无法估算.
故答案为：B. 下列说法中,正确的是( )
A. 关于某条直线对称的两个三角形是全等三角形
B. 全等的两个三角形是关于某条直线对称的
C. 两个图形关于某条直线对称,则这两个图形一定分别位于这条直线的两侧
D. 全等的两个图形一定成轴对称
A
【解析】A. 关于某条直线对称的两个三角形是全等三角形，正确；
B. 全等的两个三角形不一定关于某条直线对称，如图一，
故B错误；
C. 两个图形关于某条直线对称,则这两个图形不一定分别位于这条直线的两侧，如图二，
故C错误；
D. 全等的两个图形不一定成轴对称，如B中的图一，故D错误，
故选A. 化简或求值：（①小题4分,②小题6分,共10分）
（1）化简: 7 mn－6m－2n－（4mn+3m－2n）
（2）先化简，再求值。求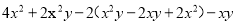
的值.
已知：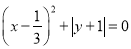 
（1）3mn-9m ；（2）3xy=-1
【解析】试题分析：（1）先去括号，然后合并同类项；（2）先根据绝对值和偶次方的非负性求出x和y的值，再把所给代数式去括号合并同类项化简，然后代入求值.
【解析】
（1）7mn－6m－2n－（4mn+3m－2n）
=7mn－6m－2n－4mn-3m+2 n
=3mn－9 m；
（2）∵,
∴=0, =0,
∴, ，... 如图，直线a、b与直线c相交，给出下列条件：①∠1＝∠5；②∠4＝∠6；
③∠4＋∠5＝180°；④∠3＋∠8＝180°；其中能判断a//b的是（ ）
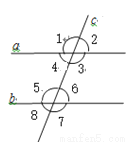
A. ①②③④ B. ①③④ C. ①③ D. ②④
A
【解析】①当∠1=∠5,则a∥b，故此选项正确；
②当∠4=∠6,则a∥b，故此选项正确；
③当∠4+∠5=180°,a∥b，故此选项正确；
④∵∠6=∠8,当∠3+∠8=180°，
∴∠3+∠6=180°，故此选项正确。
故选：A.