题目内容
7.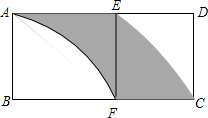 如图,矩形ABCD的长,宽之比为2:1,AF、EC为圆弧,E、F分别为AD、CB的中点,AB=a,求阴影部分的面积.
如图,矩形ABCD的长,宽之比为2:1,AF、EC为圆弧,E、F分别为AD、CB的中点,AB=a,求阴影部分的面积.
分析 由矩形的性质和已知条件证出AE=DE=AB=BF=CF=EF,四边形ABFE是正方形,得出扇形ABF的面积=扇形EFC的面积,阴影部分的面积=正方形ABFE的面积,即可得出结果.
解答 解:∵四边形ABCD是矩形,
∴AB=CD=a,AD=BC,∠B=∠BCD=∠D=90°,
∵AD:AB=2:1,
∴AD=BC=2a,
∵E、F分别为AD、CB的中点,
∴AE=DE=AB=BF=CF=EF=a,
∴扇形ABF的面积=扇形EFC的面积,四边形ABFE是正方形,
∴阴影部分的面积=正方形ABFE的面积=AB2=a2.
点评 本题考查了矩形的性质、扇形面积、正方形面积的计算;熟练掌握矩形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
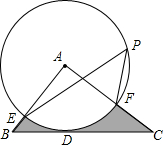 如图,在△ABC中,BC=4,以点A为圆心,2为半径的⊙A与BC相切于点D,交AB于点E,交AC于点F,点P是⊙A上的一点,且∠EPF=45°,则图中阴影部分的面积为( )
如图,在△ABC中,BC=4,以点A为圆心,2为半径的⊙A与BC相切于点D,交AB于点E,交AC于点F,点P是⊙A上的一点,且∠EPF=45°,则图中阴影部分的面积为( )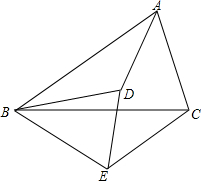 已知,如图,$\frac{AB}{BD}$=$\frac{BC}{BE}$=$\frac{CA}{ED}$,那么△ABD与△BCE相似吗?为什么?
已知,如图,$\frac{AB}{BD}$=$\frac{BC}{BE}$=$\frac{CA}{ED}$,那么△ABD与△BCE相似吗?为什么?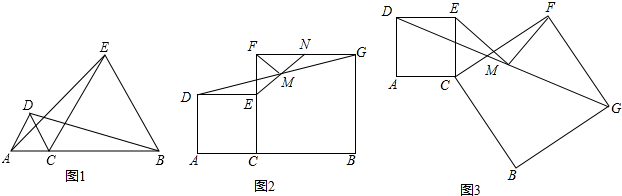
 如图,AB∥CD,直线EF分别交AB、CD于点E、F,EG平分∠AEF,∠2=100°,求∠1的度数.
如图,AB∥CD,直线EF分别交AB、CD于点E、F,EG平分∠AEF,∠2=100°,求∠1的度数.