题目内容
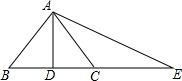如图所示，已知AD⊥BC，BD=DC，AB+BD=DE，求证：点C在AE的垂直平分线上．考点：线段垂直平分线的性质
专题：证明题
分析：首先根据AD⊥BC，BD=DC，可得AD是BC的垂直平分线，再根据AB+BD=DE可证明出AC=CE，再根据到线段两端点的距离相等的点在线段的垂直平分线上可得结论．
解答：证明：∵AD⊥BC，BD=DC，
∴AD是BC的垂直平分线，
∴AB=AC，
∵AB+BD=DE，
∴AB+BD=DC+CE，
∴AC=CE，
∴点C在AE的垂直平分线上．
∴AD是BC的垂直平分线，
∴AB=AC，
∵AB+BD=DE，
∴AB+BD=DC+CE，
∴AC=CE，
∴点C在AE的垂直平分线上．
点评：此题主要考查了线段垂直平分线的性质和判定，关键是掌握到线段两端点的距离相等的点在线段的垂直平分线上．
练习册系列答案
阅读快车系列答案
相关题目
若两数x与y的和为12，则下列说法正确的是（ ）
| A、x=1，y=11时，xy最小 |
| B、x=2，y=10时，xy最大 |
| C、x=3，y=9时，xy最大 |
| D、x=6，y=6时，xy最大 |
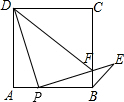如图，点P是正方形ABCD边AB上的一点（不与A、B重合），连接PD，并将线段PD绕点P顺时针旋转得到线段PE，PE交边BC于点F，连接BE、DF，∠CBE=45°，求证：DP⊥PE．