题目内容
观察下面的变形规律:
=1-
,
=
-
,
=
-
,…
解答下面的问题:
(1)若n为正整数,请你猜想
= ;
(2)证明你猜想的结论;
(3)计算:
+
+
+…+
+
.
| 1 |
| 1×2 |
| 1 |
| 2 |
| 1 |
| 2×3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3×4 |
| 1 |
| 3 |
| 1 |
| 4 |
解答下面的问题:
(1)若n为正整数,请你猜想
| 1 |
| n(n+1) |
(2)证明你猜想的结论;
(3)计算:
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 2014×2015 |
| 1 |
| 2015×2016 |
考点:有理数的混合运算
专题:规律型
分析:(1)观察已知等式,写出猜想即可;
(2)原式通分并利用同分母分式的减法法则计算,即可得证;
(3)原式利用拆项法变形后,抵消合并即可得到结果.
(2)原式通分并利用同分母分式的减法法则计算,即可得证;
(3)原式利用拆项法变形后,抵消合并即可得到结果.
解答:解:(1)
=
-
;
(2)已知等式右边=
=
=左边,得证;
(3)原式=1-
+
-
+…+
-
=1-
=
.
故答案为:(1)
=
-
.
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
(2)已知等式右边=
| n+1-n |
| n(n+1) |
| 1 |
| n(n+1) |
(3)原式=1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2015 |
| 1 |
| 2016 |
| 1 |
| 2016 |
| 2015 |
| 2016 |
故答案为:(1)
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
点评:此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
 如图,经过折叠可以围成一个
如图,经过折叠可以围成一个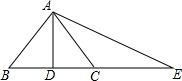 如图所示,已知AD⊥BC,BD=DC,AB+BD=DE,求证:点C在AE的垂直平分线上.
如图所示,已知AD⊥BC,BD=DC,AB+BD=DE,求证:点C在AE的垂直平分线上. 已知△ABC和点O,把△ABC绕点O顺时针旋转90°,得到△A1B1C1,在网格中画出△A1B1C1.
已知△ABC和点O,把△ABC绕点O顺时针旋转90°,得到△A1B1C1,在网格中画出△A1B1C1.