题目内容
1. 如图,在△ABC中,AB=AC=20,BC=32,点D在边BC上,且∠CAD=90°,求BD的长.
如图,在△ABC中,AB=AC=20,BC=32,点D在边BC上,且∠CAD=90°,求BD的长.
分析 过点A作AE⊥BC于点E,根据等腰三角形的性质可得出BE=BE=$\frac{1}{2}$BC,再根据勾股定理求出AE的长,设DE=x,则BD=16-x,CD=16+x,在△ADE与△ACD中根据勾股定理即可得出x的值,进而得出结论.
解答 解:点A作AE⊥BC于点E,
∵AB=AC=20,BC=32,
∴BE=CE=$\frac{1}{2}$BC.
∴AE=$\sqrt{A{C}^{2}-C{E}^{2}}$=12,
设DE=x,则BD=16-x,CD=16+x,
在Rt△ADE中,AD2=AE2+DE2,即AD2=122+x2①,
在Rt△ADC中,AD2=CD2-AC2,即AD2=(16+x)2-202②,
①②联立得,122+x2=(16+x)2-202,解得x=9,
∴BD=16-9=7.
点评 本题考查的是勾股定理的应用,在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.如果直角三角形的两条直角边长分别是a,b,斜边长为c,那么a2+b2=c2.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.下列各命题的逆命题成立的是( )
| A. | 三个内角相等的三角形是等边三角形 | |
| B. | 对顶角相等 | |
| C. | 三角形中,钝角所对的边最长 | |
| D. | 全等三角形的对应角相等 |
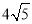 个单位长度的速度沿射线AB方向运动,过点P作PQ⊥AB,交x轴于点Q,PR∥AC交x轴于点R,设点P运动时间为t(秒),线段QR长为d,求d与t的函数关系式(不要求写出自变量t的取值范围);
个单位长度的速度沿射线AB方向运动,过点P作PQ⊥AB,交x轴于点Q,PR∥AC交x轴于点R,设点P运动时间为t(秒),线段QR长为d,求d与t的函数关系式(不要求写出自变量t的取值范围);