题目内容
10.(-$\frac{2}{3}$)×(-$\frac{2}{3}$)×(-$\frac{2}{3}$)×(-$\frac{2}{3}$)可以表示为( )| A. | (-$\frac{2}{3}$)×4 | B. | -$\frac{{2}^{4}}{3}$ | C. | -($\frac{2}{3}$)4 | D. | (-$\frac{2}{3}$)4 |
分析 原式利用乘方的意义变形即可得到结果.
解答 解:(-$\frac{2}{3}$)×(-$\frac{2}{3}$)×(-$\frac{2}{3}$)×(-$\frac{2}{3}$)=(-$\frac{2}{3}$)4,
故选D
点评 此题考查了有理数的乘方,以及有理数的乘法,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
2.下列说法正确的个数是( )
①某数的绝对值等于它本身,则此数为零或正数;
②若a≠0,b≠0,则a+b≠0;
③在数轴上到原点距离小于3的点对应的整数有5个;
④近似数2.030有4个有效数字,它们分别是2、0、3、0;
⑤若a2=9,则a=3.
①某数的绝对值等于它本身,则此数为零或正数;
②若a≠0,b≠0,则a+b≠0;
③在数轴上到原点距离小于3的点对应的整数有5个;
④近似数2.030有4个有效数字,它们分别是2、0、3、0;
⑤若a2=9,则a=3.
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
19.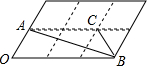 如图,6个形状、大小完全相同的菱形组成网格,菱形的顶点称为格点.已知菱形的一个角(∠O)为60°,A,B,C都在格点上,则tan∠ABC的值是( )
如图,6个形状、大小完全相同的菱形组成网格,菱形的顶点称为格点.已知菱形的一个角(∠O)为60°,A,B,C都在格点上,则tan∠ABC的值是( )
 如图,6个形状、大小完全相同的菱形组成网格,菱形的顶点称为格点.已知菱形的一个角(∠O)为60°,A,B,C都在格点上,则tan∠ABC的值是( )
如图,6个形状、大小完全相同的菱形组成网格,菱形的顶点称为格点.已知菱形的一个角(∠O)为60°,A,B,C都在格点上,则tan∠ABC的值是( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\sqrt{3}$ | D. | $\frac{2\sqrt{3}}{3}$ |


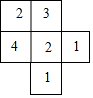 如图,是一个由小正方体搭成的几何体的俯视图,小正方形中的数字表示在该位置的正方体的个数.请你画出从正面看和从上面看到的图形(要用直尺画).
如图,是一个由小正方体搭成的几何体的俯视图,小正方形中的数字表示在该位置的正方体的个数.请你画出从正面看和从上面看到的图形(要用直尺画).