题目内容
5.已知关于x的函数y=-x2-ax+1,当0≤x≤3时函数有最大值5,则a=-4.分析 先用配方法把函数化为顶点式的形式,求出其对称轴,再根据二次函数的增减性及题目条件将顶点的横坐标的值分三种情况讨论,从而求出实数a的值.
解答 解:由原函数解析式得到:y=-(x+$\frac{a}{2}$)2+$\frac{{a}^{2}}{4}$+1,
函数的对称轴为直线x=-$\frac{a}{2}$,
顶点坐标为(-$\frac{a}{2}$,$\frac{{a}^{2}}{4}$+1).
①当0≤-$\frac{a}{2}$≤3即-6≤a≤0时,
函数最大值为5,即$\frac{{a}^{2}}{4}$+1=5,解得a=-4(舍去正值);
②当-$\frac{a}{2}$<0即a>0时,
∵当x=0时,y有最大值5,
∴y=1≠5,不合题意,舍去.
解得a=-$\frac{13}{3}$,不合题意,舍去;
③当-$\frac{a}{2}$>3即a<-6时,
∵当x=3时,y有最大值5,
∴5=-9-3a+1,
解得a=-$\frac{13}{3}$,不合题意,舍去;
综上所述,实数a的值为-4.
故答案为:-4.
点评 本题考查了求二次函数的最大(小)值的方法.注意,只有当自变量x在整个取值范围内,函数值y才在顶点处取最值.而当自变量取值范围只有一部分时,必须结合二次函数的增减性及对称轴判断何处取最大值,何处取最小值.

练习册系列答案
相关题目
13.等边三角形的边长为2,则该三角形的面积为( )
| A. | 4$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | 3 |
20.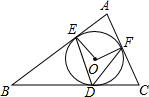 如图,⊙O内切于△ABC,切点分别为D,E,F,连接OE,OF,DE,DF,乙组∠A=80°,则∠EDF等于( )
如图,⊙O内切于△ABC,切点分别为D,E,F,连接OE,OF,DE,DF,乙组∠A=80°,则∠EDF等于( )
 如图,⊙O内切于△ABC,切点分别为D,E,F,连接OE,OF,DE,DF,乙组∠A=80°,则∠EDF等于( )
如图,⊙O内切于△ABC,切点分别为D,E,F,连接OE,OF,DE,DF,乙组∠A=80°,则∠EDF等于( )| A. | 40° | B. | 45° | C. | 50° | D. | 80° |
15.已知⊙O的直径AB=10cm,CD是⊙O的弦,CD⊥AB,垂足为M,且CD=8cm,则AC的长为( )
| A. | $2\sqrt{5}$ | B. | $2\sqrt{5}$或$4\sqrt{5}$ | C. | $4\sqrt{5}$ | D. | $2\sqrt{5}$或6 |
 如图,延长正方形ABCD的边BC至E,使CE=AC,则∠AFC=112.5°.
如图,延长正方形ABCD的边BC至E,使CE=AC,则∠AFC=112.5°.