题目内容
11．
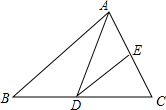如图，已知：D，E分别是△ABC的边BC和边AC的中点，连接DE，AD，若S△ABC=24cm2，则△DEC的面积的面积为（ ）| A． | 4cm2 | B． | 6cm2 | C． | 8cm2 | D． | 12cm2 |
分析 首先根据三角形的中线将三角形分成面积相等的两部分，求出S△ACD是多少；然后根据E是AC的中点，用△ACD的面积除以2，求出△DEC的面积的面积为多少即可．
解答 解：∵D是△ABC的边BC的中点，
∴S△ACD=24÷2=12（cm2）；
又∵E是AC的中点，
∴S△DEC=12÷2=6（cm2）．
故选：B．
点评 此题主要考查了三角形的面积的求法，要熟练掌握，解答此题的关键是要明确：三角形的中线将三角形分成面积相等的两部分．
练习册系列答案
相关题目
1．如果方程组$\left\{\begin{array}{l}{x+y=3}\\{5x-y=9}\end{array}\right.$的解是方程3x+my=8的一个解，则m=（ ）
| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
如图，在△ABC中，∠A=∠C，∠ABC=70°，EF∥BD，∠1=∠2，求∠ADG的度数．
如图：函数y=2x和y=ax+4的图象交于点A（m，2），不等式2x＜ax+4的解集为x＜1．
20．下列说法正确的是（ ）
| A． | $\sqrt{{{（{-2}）}^2}}$等于-2 | B． | ±$\sqrt{9}$等于3 | ||
| C． | ﹙-5﹚3的立方根是5 | D． | $\sqrt{16}$平方根是±2 |