题目内容
2.(1)如图1,AB∥CD,∠B+∠D=180°,则BC与DE平行吗?为什么?
(2)小明到工厂去进行社会实践活动时,发现工人师傅生产了一种如图2所示的零件,要求AB∥CD,∠BAE=35°,∠AED=90°.小明发现工人师傅只量出∠BAE=35°,∠AED=90°后,又量了∠EDC=55°,于是他就说AB与CD肯定是平行的,他说的对吗?为什么?
分析 (1)根据两直线平行,内错角相等可得∠B=∠C,然后求出∠C+∠D=180°,再根据同旁内角互补两直线平行证明即可;
(2)延长AE交CD与F,根据三角形的一个外角等于与它不相邻的两个内角的和∠AFD=35°,再根据内错角相等,两直线平行证明即可.
解答 (1)证明:BC与DE平行.
理由:∵AB∥CD,
∴∠B=∠C(两直线平行,内错角相等),
又∵∠B+∠D=180°(已知),
∴∠C+∠D=180°(等量代换),
∴BC∥DE(同旁内角互补,两直线平行);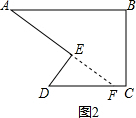 (2)解:AB与CD平行.
(2)解:AB与CD平行.
理由是:延长AE交CD于F,
∵∠AED=90°,∠EDC=55°,
∴∠AFD=∠AED-∠EDC=90°-55°=35°,
∵∠BAE=35°,
∴∠BAE=∠AFD,
∴AB∥DC.
点评 本题考查了平行线的判定与性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记性质与判定是解题的关键,难点在于(2)作出辅助线.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
13.下列二次根式是最简二次根式的是( )
| A. | $\sqrt{a+{b}^{2}}$ | B. | $\sqrt{8x}$ | C. | $\sqrt{{x}^{3}}$ | D. | $\sqrt{\frac{b}{4}}$ |
7.下列命题是假命题的是( )
| A. | 所有的实数都可以用数轴上的点表示 | |
| B. | 过直线外一点有且只有一条直线与已知直线平行 | |
| C. | 两条直线被第三条直线所截,同旁内角互补 | |
| D. | 在同一平面内,垂直于同一条直线的两条直线互相平行 |
11.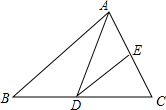 如图,已知:D,E分别是△ABC的边BC和边AC的中点,连接DE,AD,若S△ABC=24cm2,则△DEC的面积的面积为( )
如图,已知:D,E分别是△ABC的边BC和边AC的中点,连接DE,AD,若S△ABC=24cm2,则△DEC的面积的面积为( )
 如图,已知:D,E分别是△ABC的边BC和边AC的中点,连接DE,AD,若S△ABC=24cm2,则△DEC的面积的面积为( )
如图,已知:D,E分别是△ABC的边BC和边AC的中点,连接DE,AD,若S△ABC=24cm2,则△DEC的面积的面积为( )| A. | 4cm2 | B. | 6cm2 | C. | 8cm2 | D. | 12cm2 |
12.已知三角形三边长分别是1、x、2,且x为整数,那么x的取值是( )
| A. | x=1 | B. | x=2 | C. | x=3 | D. | x=4 |
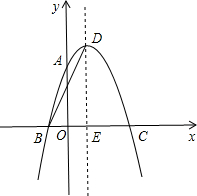 如图,抛物线y=ax2+2x+c经过点A(0,3),B(-1,0),请解答下列问题:
如图,抛物线y=ax2+2x+c经过点A(0,3),B(-1,0),请解答下列问题: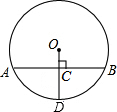 如图,在⊙O中,半径OD垂直于弦AB,垂足为C,OD=13cm,AB=24cm,则CD=8cm.
如图,在⊙O中,半径OD垂直于弦AB,垂足为C,OD=13cm,AB=24cm,则CD=8cm. 如图,Rt△ABC中,∠C=90°,AB=15,BC=9,点P,Q分别在BC,AC上,CP=3x,CQ=4x(0<x<3).把△PCQ绕点P旋转,得到△PDE,点D落在线段PQ上.
如图,Rt△ABC中,∠C=90°,AB=15,BC=9,点P,Q分别在BC,AC上,CP=3x,CQ=4x(0<x<3).把△PCQ绕点P旋转,得到△PDE,点D落在线段PQ上.