题目内容
19. 如图,在△ABC中,∠A=∠C,∠ABC=70°,EF∥BD,∠1=∠2,求∠ADG的度数.
如图,在△ABC中,∠A=∠C,∠ABC=70°,EF∥BD,∠1=∠2,求∠ADG的度数.
分析 根据三角形的内角和定理得到∠A=∠C=55°,根据EF∥BD,得到∠DBC=∠1,由于∠1=∠2,等量代换得到∠2=∠DBC,于是得到DG∥BC,即可得到结论.
解答 解:∵∠A=∠C,∠ABC=70°,
∴∠A=∠C=55°,
∵EF∥BD,
∴∠DBC=∠1,
∵∠1=∠2,
∴∠2=∠DBC,
∴DG∥BC,
∴∠ADG=∠C=55°.
点评 本题考查了平行线的判定和性质,三角形的内角和定理,熟练掌握平行线的判定和性质定理是解题的关键.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
7.下列命题是假命题的是( )
| A. | 所有的实数都可以用数轴上的点表示 | |
| B. | 过直线外一点有且只有一条直线与已知直线平行 | |
| C. | 两条直线被第三条直线所截,同旁内角互补 | |
| D. | 在同一平面内,垂直于同一条直线的两条直线互相平行 |
4.在直角坐标系中,点P(2,3)到原点的距离是( )
| A. | $\sqrt{5}$ | B. | $\sqrt{13}$ | C. | $\sqrt{11}$ | D. | 2 |
11.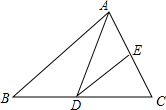 如图,已知:D,E分别是△ABC的边BC和边AC的中点,连接DE,AD,若S△ABC=24cm2,则△DEC的面积的面积为( )
如图,已知:D,E分别是△ABC的边BC和边AC的中点,连接DE,AD,若S△ABC=24cm2,则△DEC的面积的面积为( )
 如图,已知:D,E分别是△ABC的边BC和边AC的中点,连接DE,AD,若S△ABC=24cm2,则△DEC的面积的面积为( )
如图,已知:D,E分别是△ABC的边BC和边AC的中点,连接DE,AD,若S△ABC=24cm2,则△DEC的面积的面积为( )| A. | 4cm2 | B. | 6cm2 | C. | 8cm2 | D. | 12cm2 |
8.下列二次根式中,最简二次根式是( )
| A. | $\sqrt{12}$ | B. | $\sqrt{{a^2}+1}$ | C. | $\sqrt{4a}$ | D. | $\sqrt{\frac{1}{3}}$ |
 如图,一次函数y=kx+b与x轴、y轴分别交于A、B两点,则不等式kx+b>1的解集是x<0.
如图,一次函数y=kx+b与x轴、y轴分别交于A、B两点,则不等式kx+b>1的解集是x<0.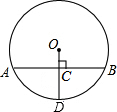 如图,在⊙O中,半径OD垂直于弦AB,垂足为C,OD=13cm,AB=24cm,则CD=8cm.
如图,在⊙O中,半径OD垂直于弦AB,垂足为C,OD=13cm,AB=24cm,则CD=8cm.