题目内容
17.用配方法解下列方程:(1)x2-4x=5;
(2)x2-100x-101=0.
分析 (1)方程变形后,利用配方法求出解即可.
(2)把常数项-101移项后,方程两边都加上2500,再把方程左边分解得到(x-50)2=2601,然后利用直接开平方法求解.
解答 解:(1)x2-4x=5,
(x-2)2=9,
x-2=±3,
解得x1=-1,x2=5;
(2)x2-100x-101=0,
x2-100x=101,
(x-50)2=2601,
x-50=±51,
解得x1=-101,x2=1.
点评 此题考查了解一元二次方程-配方法,配方法的一般步骤:(1)把常数项移到等号的右边;(2)把二次项的系数化为1;(3)等式两边同时加上一次项系数一半的平方.选择用配方法解一元二次方程时,最好使方程的二次项的系数为1,一次项的系数是2的倍数.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案
相关题目
5. 有理数a,b在数轴上的位置如图所示,则下列关系式:①|a|>|b|;②a-b>0;③a+b>0;④$\frac{1}{a}$+$\frac{1}{b}$>0;⑤-a>-b,其中正确的个数有( )
有理数a,b在数轴上的位置如图所示,则下列关系式:①|a|>|b|;②a-b>0;③a+b>0;④$\frac{1}{a}$+$\frac{1}{b}$>0;⑤-a>-b,其中正确的个数有( )
 有理数a,b在数轴上的位置如图所示,则下列关系式:①|a|>|b|;②a-b>0;③a+b>0;④$\frac{1}{a}$+$\frac{1}{b}$>0;⑤-a>-b,其中正确的个数有( )
有理数a,b在数轴上的位置如图所示,则下列关系式:①|a|>|b|;②a-b>0;③a+b>0;④$\frac{1}{a}$+$\frac{1}{b}$>0;⑤-a>-b,其中正确的个数有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
12.下列计算中,正确的是( )
| A. | $\sqrt{2}×3\sqrt{2}=4\sqrt{2}$ | B. | $\sqrt{24}$$÷\sqrt{6}$=2 | C. | $\sqrt{12}$$+\sqrt{18}$=6$\sqrt{3}$ | D. | $\sqrt{20}$-$\sqrt{5}$=4 |
7.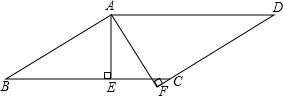 如图,在?ABCD中,AE⊥BC于点E,AF⊥DC交DC的延长线于点F,且∠EAF=35°,则∠D等于( )
如图,在?ABCD中,AE⊥BC于点E,AF⊥DC交DC的延长线于点F,且∠EAF=35°,则∠D等于( )
 如图,在?ABCD中,AE⊥BC于点E,AF⊥DC交DC的延长线于点F,且∠EAF=35°,则∠D等于( )
如图,在?ABCD中,AE⊥BC于点E,AF⊥DC交DC的延长线于点F,且∠EAF=35°,则∠D等于( )| A. | 65° | B. | 55° | C. | 35° | D. | 25° |
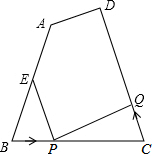 如图,在四边形ABCD中,∠B=∠C,AB=20cm.BC=15cm,点E为AB的中点,如果点P在线段BC上以5cm/秒的速度由点B向点C运动,同时,点Q在线段CD上由点C向点D运动.
如图,在四边形ABCD中,∠B=∠C,AB=20cm.BC=15cm,点E为AB的中点,如果点P在线段BC上以5cm/秒的速度由点B向点C运动,同时,点Q在线段CD上由点C向点D运动.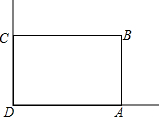 在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm、花园面积为Sm2.
在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm、花园面积为Sm2.