题目内容
12. 如图,AB为⊙O的直径,C、D为⊙O上的两点,∠BAC=∠DAC,过点C做直线EF⊥AD,交AD的延长线于点E,连接BC.
如图,AB为⊙O的直径,C、D为⊙O上的两点,∠BAC=∠DAC,过点C做直线EF⊥AD,交AD的延长线于点E,连接BC.(1)求证:EF是⊙O的切线;
(2)若DE=1,BC=2,求劣弧$\widehat{BC}$的长l.
分析 (1)连接OC,根据等腰三角形的性质得到∠OAC=∠DAC,求得∠DAC=∠OCA,推出AD∥OC,得到∠OCF=∠AEC=90°,于是得到结论;
(2)连接OD,DC,根据角平分线的定义得到∠DAC=∠OAC,根据三角函数的定义得到∠ECD=30°,得到∠OCD=60°,得到∠BOC=∠COD=60°,OC=2,于是得到结论.
解答  (1)证明:连接OC,
(1)证明:连接OC,
∵OA=OC,
∴∠OAC=∠DAC,∴∠DAC=∠OCA,
∴AD∥OC,
∵∠AEC=90°,∴∠OCF=∠AEC=90°,
∴EF是⊙O的切线;
(2)连接OD,DC,
∵∠DAC=$\frac{1}{2}∠$DOC,∠OAC=$\frac{1}{2}∠$BOC,
∴∠DAC=∠OAC,
∵ED=1,DC=2,
∴sin∠ECD=$\frac{DE}{DC}=\frac{1}{2}$,
∴∠ECD=30°,
∴∠OCD=60°,
∵OC=OD,
∴△DOC是等边三角形,
∴∠BOC=∠COD=60°,OC=2,
∴l=$\frac{60π×2}{180}$=$\frac{2}{3}$π.
点评 本题考查了切线的判定和性质,等边三角形的判定和性质,解直角三角形,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
2. 如图是一个几何体的三视图,则这个几何体是( )
如图是一个几何体的三视图,则这个几何体是( )
 如图是一个几何体的三视图,则这个几何体是( )
如图是一个几何体的三视图,则这个几何体是( )| A. |  | B. |  | C. |  | D. |  |
4.已知反比例函数y=$\frac{k}{x}$的图象过点A(1,-2),则k的值为( )
| A. | 1 | B. | 2 | C. | -2 | D. | -1 |
1.某交警在一个路口统计的某时段来往车辆的车速情况如表:
则上述车速的中位数和众数分别是( )
| 车速(km/h) | 48 | 49 | 50 | 51 | 52 |
| 车辆数(辆) | 5 | 4 | 8 | 2 | 1 |
| A. | 50,8 | B. | 50,50 | C. | 49,50 | D. | 49,8 |
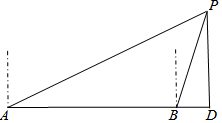 如图,一艘轮船向正东方向航行,在A处测得灯塔P在A的北偏东60°方向上,航行40海里到达B处,此时测得灯塔P在B的北偏东15°方向.求灯塔P到轮船航线的距离PD是多少海里(结果保留根号)?
如图,一艘轮船向正东方向航行,在A处测得灯塔P在A的北偏东60°方向上,航行40海里到达B处,此时测得灯塔P在B的北偏东15°方向.求灯塔P到轮船航线的距离PD是多少海里(结果保留根号)?