题目内容
20.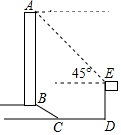 如图所示,广场有一纪念碑,其正前方恰有一个高度为15米的临时观侧台ED,从观测台顶端E处侧得纪念碑顶端A的仰角a是45°,观测台底端D到纪念碑底座边沿C的距离DC是20米,底座BC部分的坡长是12米,其坡度i=1:$\sqrt{3}$,求该纪念碑的高度.(结果精确到0.1米,参考数据:$\sqrt{2}≈1.41$,$\sqrt{3}≈1.73$,$\sqrt{6}≈2.45$)
如图所示,广场有一纪念碑,其正前方恰有一个高度为15米的临时观侧台ED,从观测台顶端E处侧得纪念碑顶端A的仰角a是45°,观测台底端D到纪念碑底座边沿C的距离DC是20米,底座BC部分的坡长是12米,其坡度i=1:$\sqrt{3}$,求该纪念碑的高度.(结果精确到0.1米,参考数据:$\sqrt{2}≈1.41$,$\sqrt{3}≈1.73$,$\sqrt{6}≈2.45$)
分析 延长AB交DC于H,作EG⊥AB于G,则GH=DE=15米,EG=DH,设BH=x米,则CH=$\sqrt{3}$x米,在Rt△BCH中,BC=12米,由勾股定理得出方程,解方程求出BH=6米,CH=6$\sqrt{3}$米,得出BG、EG的长度,证明△AEG是等腰直角三角形,得出AG=EG=6$\sqrt{3}$+20(米),即可得出纪念碑AB的高度.
解答 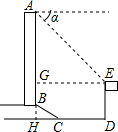 解:延长AB交DC于H,作EG⊥AB于G,如图所示:
解:延长AB交DC于H,作EG⊥AB于G,如图所示:
则GH=DE=15米,EG=DH,
∵梯坎坡度i=1:$\sqrt{3}$,
∴BH:CH=1:$\sqrt{3}$,
设BH=x米,则CH=$\sqrt{3}$x米,
在Rt△BCH中,BC=12米,
由勾股定理得:x2+($\sqrt{3}$x)2=122,
解得:x=6,
∴BH=6米,CH=6$\sqrt{3}$米,
∴BG=GH-BH=15-6=9(米),EG=DH=CH+CD=6$\sqrt{3}$+20(米),
∵∠α=45°,
∴∠EAG=90°-45°=45°,
∴△AEG是等腰直角三角形,
∴AG=EG=6$\sqrt{3}$+20(米),
∴AB=AG+BG=6$\sqrt{3}$+20+9≈39.4(米);
答:纪念碑的高度是39.4米.
点评 本题考查了解直角三角形的应用-坡度、俯角问题;通过作辅助线运用勾股定理求出BH,得出EG是解决问题的关键.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
18.在绿满鄂南行动中,咸宁市计划2015年至2017年三年间植树造林1210000亩,全力打造绿色生态旅游城市,将1210000用科学记数法表示为( )
| A. | 121×104 | B. | 12.1×105 | C. | 1.21×105 | D. | 1.21×106 |
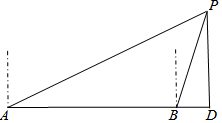 如图,一艘轮船向正东方向航行,在A处测得灯塔P在A的北偏东60°方向上,航行40海里到达B处,此时测得灯塔P在B的北偏东15°方向.求灯塔P到轮船航线的距离PD是多少海里(结果保留根号)?
如图,一艘轮船向正东方向航行,在A处测得灯塔P在A的北偏东60°方向上,航行40海里到达B处,此时测得灯塔P在B的北偏东15°方向.求灯塔P到轮船航线的距离PD是多少海里(结果保留根号)?