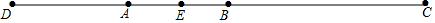��Ŀ����
20��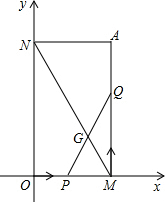 ��ͼ����֪����A��2��4���ֱ���x�ᡢy��Ĵ��ߣ�����ֱ�ΪM��N������P��O���������OM�������˶���1���ӿɵ���M�㣬��Q��M���������MA�������˶���1���ӿɵ���A�㣮��PQ��MN���ڵ�G��
��ͼ����֪����A��2��4���ֱ���x�ᡢy��Ĵ��ߣ�����ֱ�ΪM��N������P��O���������OM�������˶���1���ӿɵ���M�㣬��Q��M���������MA�������˶���1���ӿɵ���A�㣮��PQ��MN���ڵ�G����1����������ʱ�䣬�߶�PQ�ij���Ϊ2��
��2��д���߶�PQ���ȵ�ƽ��y��ʱ��t֮��ĺ�����ϵʽ��
��3���о���������ʱ��t��ʹP��Q��M���ɵ����������MON���ƣ������ʱ��t����ֱ�Ӹ�����ʱ��GPM����״��
���� ��1�������������P��Q�����ƶ����ٶȣ����辭��t���ӣ��߶�PQ�ij���Ϊ2����y��ʾ��PM��QM�ij����ɹ��ɶ����������t��ֵ��
��2���ɣ�1����PM��QM�ij��ȼ��ɵó��߶�PQ���ȵ�ƽ����y��ʱ��t֮��ĺ�����ϵʽ��t��ȡֵ��Χ��
��3�����������������εĶ�Ӧ�߲���ȷ������Ӧ����������������ۣ�
��� �⣺��1����A��2��4������OM=AN=2��AM=ON=4��
��P��1���ӿɵ���M�㣬Q��1���ӿɵ���A�㣬
��P����˶��ٶ���2����λÿ���ӣ�Q����˶��ٶ���4����λÿ���ӣ�
�辭��t�룬��PM=2-2t��MQ=4t��
��Rt��PQM��PM2+MQ2=PQ2������2-2t��2+16t2=4��
20t2-4t=0�����t=$\frac{2}{5}$��0����ȥ����
������$\frac{2}{5}$�룬�߶�PQ�ij���Ϊ2��
��2���ɣ�1����֪��PM=2-2t��QM=4t��
��Rt��PQM��PQ2=PM2+QM2��
��y=��2-2t��2+16t2��
��y=20t2-8t+4��
��3������PMQ�ס�MONʱ��
$\frac{PM}{OM}$=$\frac{MQ}{ON}$��
��$\frac{2-2t}{2}$=$\frac{4t}{4}$��
��ã�t=$\frac{1}{2}$��
����QMP�ס�MONʱ��
$\frac{QM}{OM}$=$\frac{MP}{ON}$��
��$\frac{4t}{2}$=$\frac{2-2t}{4}$��
��ã�t=$\frac{1}{5}$��
�ʵ�t=$\frac{1}{2}$��$\frac{1}{2}$ʱ��P��Q��M���ɵ����������MON���ƣ�
���� ���⿼������������ۺ��⣬�漰�����������ε����ʼ����ɶ���������������t��ʾ��PM��QM�ij����ǽ�����Ĺؼ���

 ���ĺ����Ͼ�������ϵ�д�
���ĺ����Ͼ�������ϵ�д�| A�� | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B�� | $\sqrt{2}$��$\sqrt{8}$=4 | C�� | $\sqrt{6}$��$\sqrt{5}$=$\frac{\sqrt{6}}{5}$ | D�� | $\sqrt{��-3��^{2}}$=-3 |
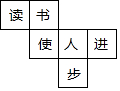 Сǿ������һ��������ģ�͵�չ��ͼ����ͼ��ʾ���ѡ�����ʹ�˽����������ֱַ�ճ�����������ϣ���ô��������ģ�����롰�顱��Ե����ϵ����ǣ�������
Сǿ������һ��������ģ�͵�չ��ͼ����ͼ��ʾ���ѡ�����ʹ�˽����������ֱַ�ճ�����������ϣ���ô��������ģ�����롰�顱��Ե����ϵ����ǣ�������| A�� | ʹ | B�� | �� | C�� | �� | D�� | �� |
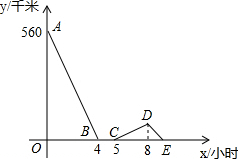 һ��������һ���쳵�ֱ�Ӽס�������ͬʱ����������������У�������;��������ͣ��һ��ʱ�䣬Ȼ��ֱ�ԭ��һͬʻ���غ�ͣ������������ʻ��ʱ��ΪxСʱ������֮��ľ���Ϊyǧ�ף�ͼ�����߱�ʾy��x֮��ĺ���ͼ�������ͼ�����������⣺
һ��������һ���쳵�ֱ�Ӽס�������ͬʱ����������������У�������;��������ͣ��һ��ʱ�䣬Ȼ��ֱ�ԭ��һͬʻ���غ�ͣ������������ʻ��ʱ��ΪxСʱ������֮��ľ���Ϊyǧ�ף�ͼ�����߱�ʾy��x֮��ĺ���ͼ�������ͼ�����������⣺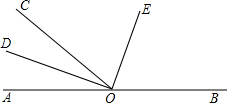 ��ͼ����OΪֱ��AB�ϵ�һ�㣬��BOC=130�㣬OEƽ�֡�BOC��DO��OE��
��ͼ����OΪֱ��AB�ϵ�һ�㣬��BOC=130�㣬OEƽ�֡�BOC��DO��OE��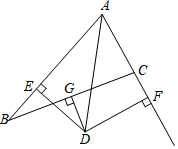 ��ͼ���ڡ�ABC�У�AB=7��AC=3��GΪBC���е㣬DG��BC����BAC��ƽ����AD��D��DE��AB��E��DF��AC��F��AC���ӳ�����F������˵����ȷ���ǣ�������
��ͼ���ڡ�ABC�У�AB=7��AC=3��GΪBC���е㣬DG��BC����BAC��ƽ����AD��D��DE��AB��E��DF��AC��F��AC���ӳ�����F������˵����ȷ���ǣ�������