题目内容
 如图,△ABC中,AD是高,E、F分别是AB、AC的中点.
如图,△ABC中,AD是高,E、F分别是AB、AC的中点.(1)若AB=10,AC=8,求四边形AEDF的周长;
(2)求证:EF垂直平分AD.
考点:直角三角形斜边上的中线,线段垂直平分线的性质
专题:
分析:(1)根据直角三角形斜边上的中线等于斜边的一半可得DE=AE=
AB,DF=AF=
AC,再根据四边形的周长的定义计算即可得解;
(2)根据到到线段两端点距离相等的点在线段的垂直平分线上证明即可.
| 1 |
| 2 |
| 1 |
| 2 |
(2)根据到到线段两端点距离相等的点在线段的垂直平分线上证明即可.
解答:(1)解:∵AD是高,E、F分别是AB、AC的中点,
∴DE=AE=
AB=
×10=5,DF=AF=
AC=
×8=4,
∴四边形AEDF的周长=AE+DE+DF+AF=5+5+4+4=18;
(2)证明:∵DE=AE,DF=AF,
∴EF垂直平分AD.
∴DE=AE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴四边形AEDF的周长=AE+DE+DF+AF=5+5+4+4=18;
(2)证明:∵DE=AE,DF=AF,
∴EF垂直平分AD.
点评:本题考查了直角三角形斜边上的中线等于斜边的一半的性质,到线段两端点距离相等的点在线段的垂直平分线上,熟记性质与线段垂直平分线的判定方法是解题得解.

练习册系列答案
相关题目
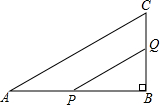 在△ACB中,∠B=90°,AB=6cm,BC=3cm,点P从A点开始沿着AB边向点B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动,如果P、Q分别从A、B同时出发:
在△ACB中,∠B=90°,AB=6cm,BC=3cm,点P从A点开始沿着AB边向点B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动,如果P、Q分别从A、B同时出发:
 如图,在Rt△ABC中,∠C=90°,AC=12,BC=9,AB的垂直平分线分别交AB、AC于点D、E.
如图,在Rt△ABC中,∠C=90°,AC=12,BC=9,AB的垂直平分线分别交AB、AC于点D、E. 问题:如图,点C是线段AB的中点,点D在线段CB上,点E是线段AD的中点.若EC=8,求线段DB的长.请补全以下解答过程.
问题:如图,点C是线段AB的中点,点D在线段CB上,点E是线段AD的中点.若EC=8,求线段DB的长.请补全以下解答过程.