题目内容
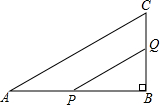 在△ACB中,∠B=90°,AB=6cm,BC=3cm,点P从A点开始沿着AB边向点B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动,如果P、Q分别从A、B同时出发:
在△ACB中,∠B=90°,AB=6cm,BC=3cm,点P从A点开始沿着AB边向点B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动,如果P、Q分别从A、B同时出发:(1)经过多长时间,S△PQB=
| 1 |
| 2 |
(2)经过多长时间,P、Q间的距离等于4
| 2 |
考点:一元二次方程的应用
专题:几何动点问题
分析:(1)设经过了x秒,S△PQB=
S△ABC,则可得到AP=xcm,BQ=2xcm,BP=(6-x)cm,利用三角形的面积列出方程求得x的值即可;
(2)设经过y秒,PQ=4
cm,则AP=ycm,BQ=2ycm,BP=(6-y)cm,利用勾股定理列出方程即可求解.
| 1 |
| 2 |
(2)设经过y秒,PQ=4
| 2 |
解答:解:(1)设经过了x秒,S△PQB=
S△ABC,
∴AP=xcm,BQ=2xcm,BP=(6-x)cm,
∴
(6-x)•2x=
×
×6×3
整理得:2x2-12x+9=0
解得:x=
或x=
∵AP≤6cm,BQ≤3cm,
所以x=
;
(2)设经过y秒,PQ=4
cm,
则AP=ycm,BQ=2ycm,BP=(6-y)cm,
∴(2y)2+(6-y)2=(4
)2
解得:y=2或y=
经检验y=2不合题意,舍去,故y=
| 1 |
| 2 |
∴AP=xcm,BQ=2xcm,BP=(6-x)cm,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
整理得:2x2-12x+9=0
解得:x=
6+3
| ||
| 2 |
6-3
| ||
| 2 |
∵AP≤6cm,BQ≤3cm,
所以x=
6-3
| ||
| 2 |
(2)设经过y秒,PQ=4
| 2 |
则AP=ycm,BQ=2ycm,BP=(6-y)cm,
∴(2y)2+(6-y)2=(4
| 2 |
解得:y=2或y=
| 2 |
| 5 |
经检验y=2不合题意,舍去,故y=
| 2 |
| 5 |
点评:本题考查了一元二次方程的应用,解题的关键是正确的设出未知数并表示出有关线段的长.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列命题是真命题的是( )
| A、两边及一个角对应相等的两三角形全等 |
| B、两角及一边对应相等的两三角形全等 |
| C、三个角对应相等的两三角形全等 |
| D、面积相等的两三角形全等 |
 请你在图中画出在点O的:
请你在图中画出在点O的:
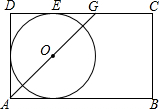 如图,矩形ABCD,∠DAB的平分线交DC于点G,O是AG的中点,⊙O与DG相切,切点为E,
如图,矩形ABCD,∠DAB的平分线交DC于点G,O是AG的中点,⊙O与DG相切,切点为E, 如图:直线y=kx+3与x轴、y轴分别交于A、B两点,
如图:直线y=kx+3与x轴、y轴分别交于A、B两点, 如图,△ABC中,AD是高,E、F分别是AB、AC的中点.
如图,△ABC中,AD是高,E、F分别是AB、AC的中点.