题目内容
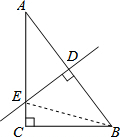
如图，在Rt△ABC中，∠C=90°，AC=12，BC=9，AB的垂直平分线分别交AB、AC于点D、E．（1）求线段AB的长；
（2）求线段AE的长．
考点：线段垂直平分线的性质,勾股定理
专题：
分析：（1）根据勾股定理求出即可；
（2）根据线段垂直平分线求出AE=BE，根据勾股定理得出方程，求出方程的解即可．
（2）根据线段垂直平分线求出AE=BE，根据勾股定理得出方程，求出方程的解即可．
解答：解：（1）在Rt△ABC中，∠C=90°，AC=12，BC=9，由勾股定理得：AB=
=15；
（2）
连接BE，
∵AB的垂直平分线DE，
∴AE=BE，
设AE=x，则BE=x，CE=12-x，
在Rt△BCE中，由勾股定理得：（12-x）2+92=x2，
解得：x=
，
即AE=
．
| 122+92 |
（2）
连接BE，
∵AB的垂直平分线DE，
∴AE=BE，
设AE=x，则BE=x，CE=12-x，
在Rt△BCE中，由勾股定理得：（12-x）2+92=x2，
解得：x=
| 75 |
| 8 |
即AE=
| 75 |
| 8 |
点评：本题考查了线段垂直平分线性质和勾股定理的应用，此题是一道比较好的题目，难度适中，注意：线段垂直平分线上的点到线段两个端点的距离相等．
练习册系列答案
阅读快车系列答案
相关题目
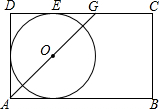如图，矩形ABCD，∠DAB的平分线交DC于点G，O是AG的中点，⊙O与DG相切，切点为E，
问题引入：
如图，△ABC中，AD是高，E、F分别是AB、AC的中点．
如图，公园要在一个圆形的喷水池中央垂直于水面处安装一个柱子OA，O恰在水面中心，OA=1.25m，由柱子顶端A处的喷头向外喷水，水流在各个方向沿形状相同的抛物线路线落下，为使水流形状较为漂亮，要求设计成水流在离OA的距离为1m处达到距水面的距离最大，高度为2.25m．若不计其它因素，那么水池的半径至少要多少米才能使喷出的水流不致落到池外？