题目内容
 问题:如图,点C是线段AB的中点,点D在线段CB上,点E是线段AD的中点.若EC=8,求线段DB的长.请补全以下解答过程.
问题:如图,点C是线段AB的中点,点D在线段CB上,点E是线段AD的中点.若EC=8,求线段DB的长.请补全以下解答过程.解:∵点C是线段AB的中点,
∴AB=2AC,AD=2AE.
∵DB=AB-
∴DB=
∵EC=8,
∴DB=
考点:两点间的距离
专题:推理填空题
分析:先根据点C是线段AB的中点,点E是线段AD的中点,得到AB=2AC,AD=2AE,再根据DB=AB-AD,等量代换可得DB=2EC,进而求出线段DB的长.
解答:解:∵点C是线段AB的中点,点E是线段AD的中点,
∴AB=2AC,AD=2AE.
∵DB=AB-
,
∴DB=
-2AE=2(AC-AE)=2EC.
∵EC=8,
∴DB=
.
∴AB=2AC,AD=2AE.
∵DB=AB-
| AD |
. |
∴DB=
| 2AC |
. |
∵EC=8,
∴DB=
| 16 |
. |
点评:本题考查的是两点间的距离,解答此类问题时要注意各线段之间的和、差关系.

练习册系列答案
相关题目
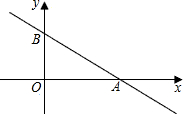 如图:直线y=kx+3与x轴、y轴分别交于A、B两点,
如图:直线y=kx+3与x轴、y轴分别交于A、B两点, 已知一次函数y=kx-3的图象与正比例函数
已知一次函数y=kx-3的图象与正比例函数 如图,△ABC中,AD是高,E、F分别是AB、AC的中点.
如图,△ABC中,AD是高,E、F分别是AB、AC的中点. 在一条笔直的公路上有A、B两地,甲骑自行车从A地到B地;乙骑自行车从B地到A地,到达A地后立即按原路返回,如图是甲、乙两人离B地的距离y(km)与行驶时间x(h)之间的函数图象,根据图象解答以下问题:
在一条笔直的公路上有A、B两地,甲骑自行车从A地到B地;乙骑自行车从B地到A地,到达A地后立即按原路返回,如图是甲、乙两人离B地的距离y(km)与行驶时间x(h)之间的函数图象,根据图象解答以下问题: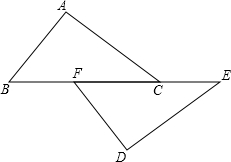 如图,已知:点B、F、C、E在一条直线上,∠B=∠E,BF=CE,AC∥DF.求证:△ABC≌△DEF.
如图,已知:点B、F、C、E在一条直线上,∠B=∠E,BF=CE,AC∥DF.求证:△ABC≌△DEF.