题目内容
6.计算:(1)(-x)•x2•(-x)6
(2)(y4)2÷(y2)3•y2
(3)(-2a)3-(-a)•(3a)2
(4)(x-y)3•(x-y)2•(y-x)
(5)($\frac{1}{2}$)-2-23×0.125+20140
(6)($\frac{1}{2}$)2013×(-2)2014.
分析 (1)(4)根据同底数幂的乘法法则计算即可求解;
(2)先算积的乘方,再算同底数幂的乘除法;
根据多项式除以单项式的计算法则计算即可求解;
(3)先算积的乘方,再算同底数幂的乘法,再合并同类项即可求解;
(5)先计算负整数指数幂,乘方,零指数幂,再计算加减法即可求解;
(6)逆用积的乘方即可求解.
解答 解:(1)(-x)•x2•(-x)6=-x9;
(2)(y4)2÷(y2)3•y2
=y8÷y6•y2
=y4;
(3)(-2a)3-(-a)•(3a)2
=-8a3-(-a)•9a2
=-8a3+9a3
=a3;
(4)(x-y)3•(x-y)2•(y-x)
=-(x-y)3+2+1
=-(x-y)6;
(5)($\frac{1}{2}$)-2-23×0.125+20140
=4-8×0.125+1
=4-1+1
=4;
(6)($\frac{1}{2}$)2013×(-2)2014.
=(-$\frac{1}{2}$×2)2013×(-2)
=(-1)2013×(-2)
=-1×(-2)
=2.
点评 考查了整式的混合运算,注意:(1)有乘方、乘除的混合运算中,要按照先乘方后乘除的顺序运算,其运算顺序和有理数的混合运算顺序相似.(2)“整体”思想在整式运算中较为常见,适时采用整体思想可使问题简单化,并且迅速地解决相关问题,此时应注意被看做整体的代数式通常要用括号括起来.同时考查了实数的运算.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,将一副三角板放在一块,AC与EF所夹的钝角的度数为165°.
如图,将一副三角板放在一块,AC与EF所夹的钝角的度数为165°.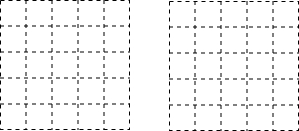
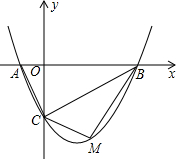 如图,二次函数y=ax2-$\frac{3}{2}$x+c(a≠0)的图象与x轴交于A、B两点,与y轴交于C点,已知点A(-1,0),点C(0,-2).
如图,二次函数y=ax2-$\frac{3}{2}$x+c(a≠0)的图象与x轴交于A、B两点,与y轴交于C点,已知点A(-1,0),点C(0,-2).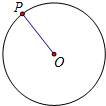 如图所示,⊙O的面积为1,点P为⊙O上一点,令记号[n,m]表示半径OP从如图所示的位置开始以点O为中心连续旋转n次后,半径OP扫过的面积.旋转的规则为:第1次旋转m度;第2次从第1次停止的位置向相同的方向再次旋转$\frac{m}{2}$度;第3次从第2次停止的位置向相同的方向再次旋转$\frac{m}{4}$度;第4次从第3次停止的位置向相同的方向再次旋转$\frac{m}{8}$度;…依此类推.例如[2,90]=$\frac{3}{8}$,则[2016,180]=$\frac{{2}^{2016}-1}{{2}^{2016}}$.
如图所示,⊙O的面积为1,点P为⊙O上一点,令记号[n,m]表示半径OP从如图所示的位置开始以点O为中心连续旋转n次后,半径OP扫过的面积.旋转的规则为:第1次旋转m度;第2次从第1次停止的位置向相同的方向再次旋转$\frac{m}{2}$度;第3次从第2次停止的位置向相同的方向再次旋转$\frac{m}{4}$度;第4次从第3次停止的位置向相同的方向再次旋转$\frac{m}{8}$度;…依此类推.例如[2,90]=$\frac{3}{8}$,则[2016,180]=$\frac{{2}^{2016}-1}{{2}^{2016}}$.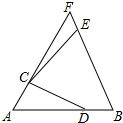 如图,等边△ABF中,点C,D分别在AF、AB上,线段CD绕点C逆时针旋转60°到线段CE,点E恰好落在BF上.
如图,等边△ABF中,点C,D分别在AF、AB上,线段CD绕点C逆时针旋转60°到线段CE,点E恰好落在BF上.