题目内容
15. 如图,已知线段AB上有两点C、D,且AC=BD,M,N分别是线段AC,AD的中点,若AB=acm,AC=BD=bcm,且a、b满足(a-10)2+|$\frac{b}{2}$-4|=0.
如图,已知线段AB上有两点C、D,且AC=BD,M,N分别是线段AC,AD的中点,若AB=acm,AC=BD=bcm,且a、b满足(a-10)2+|$\frac{b}{2}$-4|=0.(1)求a、b的值;
(2)求线段MN的长度.
分析 (1)由偶次方及绝对值的非负性即可得出a-10=0、$\frac{b}{2}$-4=0,解之即可得出a、b的值;
(2)由AB、BD的长度即可求出AD的长度,根据M、N分别是线段AC、AD的中点即可求出AM、AN的长度,再根据MN=AM-AN即可求出MN的长度.
解答 解:(1)∵(a-10)2+|$\frac{b}{2}$-4|=0.
∴a-10=0,$\frac{b}{2}$-4=0,
∴a=10,b=8.
(2)∵BD=AC=8cm,
∴AD=AB-BD=2cm.
又∵M、N分别是线段AC、AD的中点,
∴AM=4cm,AN=1cm,
∴MN=AM-AN=3cm.
点评 本题考查了两点间的距离、绝对值及偶次方的非负性,解题的关键是:(1)根据偶次方及绝对值的非负性求出a、b值;(2)根据M、N分别是线段AC、AD的中点求出AM、AN的长度.

练习册系列答案
相关题目
7.-$\frac{1}{2014}$的绝对值的相反数是( )
| A. | -2014 | B. | $\frac{1}{2014}$ | C. | 2014 | D. | $-\frac{1}{2014}$ |
4.下列说法正确的是( )
| A. | 任何一个有理数的绝对值都是正数 | |
| B. | 有理数可以分为正有理数和负有理数 | |
| C. | 多项式3πa3+4a2-8的次数是4 | |
| D. | x的系数和次数都是1 |
5. 如图,⊙O是四边形ABCD的外接圆,若∠O=110°,则∠C的度数为( )
如图,⊙O是四边形ABCD的外接圆,若∠O=110°,则∠C的度数为( )
 如图,⊙O是四边形ABCD的外接圆,若∠O=110°,则∠C的度数为( )
如图,⊙O是四边形ABCD的外接圆,若∠O=110°,则∠C的度数为( )| A. | 125° | B. | 120° | C. | 105° | D. | 90° |
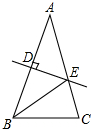 如图,在△ABC中,AB=AC,AB的垂直平分线交AC于点E,垂足为D,连接BE,若BC=4cm,△BEC的周长为10cm,则AB的长为6cm.
如图,在△ABC中,AB=AC,AB的垂直平分线交AC于点E,垂足为D,连接BE,若BC=4cm,△BEC的周长为10cm,则AB的长为6cm.