题目内容
5．化简：（1）（x+2y）2-（x+2y）（x-2y）；
（2）$\frac{x}{{x}^{2}-9}$÷（$\frac{2}{3+x}$+$\frac{1}{3-x}$-1）
分析 （1）先根据完全平方公式和平方差公式展开，再去括号、合并可得；
（2）先将分母因式分解，计算括号内异分母分式加减，再计算除法即可得．
解答 解：（1）原式=x2+4xy+4y2-（x2-4y2）
=x2+4xy+4y2-x2+4y2
=4xy+8y2；
（2）原式=$\frac{x}{（x+3）（x-3）}$÷$\frac{2x-6-x-3-{x}^{2}+9}{（x+3）（x-3）}$
=$\frac{x}{（x+3）（x-3）}$•$\frac{（x+3）（x-3）}{x（1-x）}$
=$\frac{1}{1-x}$．
点评 本题主要考查分式的化简和整式的化简，熟练掌握完全平方公式和平方差公式及分式的混合运算顺序、法则是解题的关键．
练习册系列答案
捷径训练检测卷系列答案
小夫子全能检测系列答案
相关题目
2．二次函数y=-3x2+6x变形为y=a（x+m）2+n形式，正确的是（ ）
| A． | y=-3（x+1）2-3 | B． | y=-3（x-1）2-3 | C． | y=-3（x+1）2+3 | D． | y=-3（x-1）2+3 |
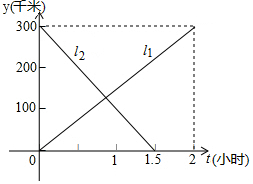厦深铁路开通后，直线l1与l2分别表示从深圳北开往潮阳站的动车和从潮阳站开往深圳的高铁，两车同时出发，设动车离深圳北的距离为y1（千米），高铁离深圳的距离为距离y2（千米），行驶时间为t（小时），与t的函数关系如图所示：
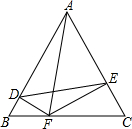如图，△ABC是边长为8的等边三角形，F是边BC上的动点，且DF⊥AB，EF⊥AC．则四边形ADFE的面积最大值是12$\sqrt{3}$．
如图，已知线段AB上有两点C、D，且AC=BD，M，N分别是线段AC，AD的中点，若AB=acm，AC=BD=bcm，且a、b满足（a-10）2+|$\frac{b}{2}$-4|=0．