题目内容
3.观察下列各式:$\frac{1}{2}$×$\frac{2}{3}$=$\frac{1}{3}$
$\frac{1}{2}$×$\frac{2}{3}$×$\frac{3}{4}$=$\frac{1}{4}$
$\frac{1}{2}$×$\frac{2}{3}$×$\frac{3}{4}$×$\frac{4}{5}$=$\frac{1}{5}$
…
(1)猜想$\frac{1}{2}$×$\frac{2}{3}$×$\frac{3}{4}$×…×$\frac{n}{n+1}$=$\frac{1}{n+1}$;
(2)根据上面的规律,解答下列问题:
①($\frac{1}{100}$-1)×($\frac{1}{99}$-1)×($\frac{1}{98}$-1)×…×($\frac{1}{4}$-1)×($\frac{1}{3}$-1)×($\frac{1}{2}$-1)
②将2016减去它的$\frac{1}{2}$,再减去余下的$\frac{1}{3}$,再减去余下的$\frac{1}{4}$,再减去余下的$\frac{1}{5}$,以此类推,直到最后减去余下的$\frac{1}{2016}$,最后结果是多少?
分析 (1)根据所给各式发现规律,结果的分子为第1个分数的分子,分母为最后1个分数的分母;
(2)原式括号中变形计算后,约分即可得到结果;
(3)根据题意列出算式,计算即可得到结果.
解答 解:(1)∵$\frac{1}{2}$×$\frac{2}{3}$=$\frac{1}{3}$
$\frac{1}{2}$×$\frac{2}{3}$×$\frac{3}{4}$=$\frac{1}{4}$
$\frac{1}{2}$×$\frac{2}{3}$×$\frac{3}{4}$×$\frac{4}{5}$=$\frac{1}{5}$
…
∴$\frac{1}{2}$×$\frac{2}{3}$×$\frac{3}{4}$×…×$\frac{n}{n+1}$=$\frac{1}{n+1}$
故答案为:$\frac{1}{n+1}$;
(2)①原式=-$\frac{99}{100}$×($-\frac{98}{99}$)×(-$\frac{97}{98}$)×…×(-$\frac{2}{3}$)×(-$\frac{1}{2}$)
=-$\frac{1}{100}$;
②由题意得,2016×(1-$\frac{1}{2}$)×(1-$\frac{1}{3}$)×…×(1-$\frac{1}{2016}$)=2016×$\frac{1}{2016}$
=1.
点评 此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.把抛物线y=-4x2的图象向左平移3个单位长度,得到的抛物线的解析式是( )
| A. | y=-4x2-3 | B. | y=-4(x+3)2 | C. | y=-4(x-3)2 | D. | y=-4x2+3 |
8.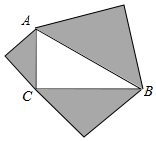 如图,分别以Rt△ABC的三边为斜边向外作等腰直角三角形,若斜边AB=4,则图中阴影部分的面积为( )
如图,分别以Rt△ABC的三边为斜边向外作等腰直角三角形,若斜边AB=4,则图中阴影部分的面积为( )
 如图,分别以Rt△ABC的三边为斜边向外作等腰直角三角形,若斜边AB=4,则图中阴影部分的面积为( )
如图,分别以Rt△ABC的三边为斜边向外作等腰直角三角形,若斜边AB=4,则图中阴影部分的面积为( )| A. | 4 | B. | 8 | C. | 10 | D. | 12 |
12.我国第一艘航母最大排水量为67500吨,用科学记数法表示这个数字是( )
| A. | 6.75×104吨 | B. | 67.5×103吨 | C. | 6.75×103吨 | D. | 6.75×105吨 |
 如图,已知线段AB上有两点C、D,且AC=BD,M,N分别是线段AC,AD的中点,若AB=acm,AC=BD=bcm,且a、b满足(a-10)2+|$\frac{b}{2}$-4|=0.
如图,已知线段AB上有两点C、D,且AC=BD,M,N分别是线段AC,AD的中点,若AB=acm,AC=BD=bcm,且a、b满足(a-10)2+|$\frac{b}{2}$-4|=0.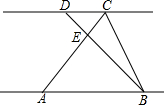 如图,已知AB∥CD,AB=2$\sqrt{3}$,CD=2$\sqrt{2}$,S△ABE=3,S△BCE=$\sqrt{6}$,求S△CDE.
如图,已知AB∥CD,AB=2$\sqrt{3}$,CD=2$\sqrt{2}$,S△ABE=3,S△BCE=$\sqrt{6}$,求S△CDE.