题目内容
17.已知二次函数y=x2-4mx+m-$\frac{1}{2}$的图象经过原点O,与x轴相交于另一点A,抛物线的顶点为B,则△OAB的面积是( )| A. | 2 | B. | $\frac{1}{2}$ | C. | 1 | D. | $\frac{3}{2}$ |
分析 根据题意确定出A与B的坐标,进而求出三角形OAB面积.
解答 解:把(0,0)代入二次函数解析式得:0=m-$\frac{1}{2}$,
解得:m=$\frac{1}{2}$,即y=x2-2x,顶点坐标为(1,-1),
令y=0,得到x(x-2)=0,
解得:x=0或x=2,即A坐标为(2,0),OA=2,
则△OAB的面积S=$\frac{1}{2}$×2×1=1,
故选C
点评 此题考查了抛物线与x轴的交点,抛物线图象是否与x轴相交与根的判别式有关.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.若|a|>-a,则( )
| A. | a>0 | B. | a<0 | C. | a<-1 | D. | 1<a |
12.一元二次方程x2+4x-1=0的两根之积是( )
| A. | 4 | B. | -4 | C. | 1 | D. | -1 |
2. 如图,数轴上A、B两点分别对应有理数a,b,则下列四个数中最大的是( )
如图,数轴上A、B两点分别对应有理数a,b,则下列四个数中最大的是( )
 如图,数轴上A、B两点分别对应有理数a,b,则下列四个数中最大的是( )
如图,数轴上A、B两点分别对应有理数a,b,则下列四个数中最大的是( )| A. | a | B. | b | C. | -a | D. | -b |
6.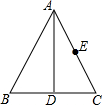 如图,在等边△ABC中,AD平分∠BAC交BC与点D,点E为AC边的中点,BC=2;在AD上有一动点Q,则QC+QE的最小值为( )
如图,在等边△ABC中,AD平分∠BAC交BC与点D,点E为AC边的中点,BC=2;在AD上有一动点Q,则QC+QE的最小值为( )
 如图,在等边△ABC中,AD平分∠BAC交BC与点D,点E为AC边的中点,BC=2;在AD上有一动点Q,则QC+QE的最小值为( )
如图,在等边△ABC中,AD平分∠BAC交BC与点D,点E为AC边的中点,BC=2;在AD上有一动点Q,则QC+QE的最小值为( )| A. | $\sqrt{3}$ | B. | 1.5 | C. | $\sqrt{2}$ | D. | 1 |
7.已知a、b互为相反数,c、d互为倒数,|m|=3,则代数式$\frac{a+b}{cd}$+m的值为( )
| A. | ±2 | B. | -3 | C. | 3 | D. | ±3 |
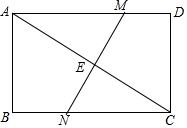 如图,在矩形ABCD中,AC是对角线,AC的中垂线MN交AD于M,交BC于N,AB=6,BC=8,求MN的长.
如图,在矩形ABCD中,AC是对角线,AC的中垂线MN交AD于M,交BC于N,AB=6,BC=8,求MN的长.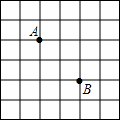 如图,A,B在格点位置上,若要在所给的网络中再找一个格点,使它与点A,B连成的三角形是轴对称图形,那么图中满足这样条件的格点格点共有( )
如图,A,B在格点位置上,若要在所给的网络中再找一个格点,使它与点A,B连成的三角形是轴对称图形,那么图中满足这样条件的格点格点共有( )