题目内容
 在平面直角坐标系中,如图,将线段AB平移至线段CD,连接AC、BD.
在平面直角坐标系中,如图,将线段AB平移至线段CD,连接AC、BD. ①直接写出图中相等的线段、平行的线段;
②已知A(-3,0)、B(-2,-2),点C在y轴的正半轴上,点D在第一象限内,且S△ACO=5,求点C、D的坐标.
考点:坐标与图形变化-平移,三角形的面积
专题:
分析:①根据平移变换只改变图形的位置不改变图形的形状可知对应相等平行且相等,对应点的连线平行且相等;
②由点A和点C在y轴上确定出向右平移3个单位,再根据△ACD的面积求出向上平移的单位,然后写出点C、D的坐标即可.
②由点A和点C在y轴上确定出向右平移3个单位,再根据△ACD的面积求出向上平移的单位,然后写出点C、D的坐标即可.
解答:解:①AB=CD,BD=AC,AB∥CD,BD∥AC;
②∵A(-3,0),点C在y轴的正半轴上,
∴向右平移3个单位,
设向上平移x个单位,
∵S△ACO=5,
∴
×3x=5,
解得x=
,
∴点C的坐标为(0,
),
-2+3=1,-2+
=
,
故点D的坐标为(1,
).
②∵A(-3,0),点C在y轴的正半轴上,
∴向右平移3个单位,
设向上平移x个单位,
∵S△ACO=5,
∴
| 1 |
| 2 |
解得x=
| 10 |
| 3 |
∴点C的坐标为(0,
| 10 |
| 3 |
-2+3=1,-2+
| 10 |
| 3 |
| 4 |
| 3 |
故点D的坐标为(1,
| 4 |
| 3 |
点评:本题考查了坐标与图形变化-平移,三角形的面积,熟记平移变化只改变图形的位置不改变图形的形状是解题的关键.

练习册系列答案
相关题目
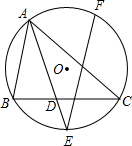 如图,圆的内接△ABC中,∠BAC的平分线AD的延长线交⊙O于点E,过点E作弦EF,使EF=AC,求证:EF∥AB.
如图,圆的内接△ABC中,∠BAC的平分线AD的延长线交⊙O于点E,过点E作弦EF,使EF=AC,求证:EF∥AB.
 在△ABC中,∠ACB=90°,CE⊥AB于点E,D在AB延长线上,且∠DCB=∠A,BD:CD=1:2,AE=
在△ABC中,∠ACB=90°,CE⊥AB于点E,D在AB延长线上,且∠DCB=∠A,BD:CD=1:2,AE=