题目内容
19.下列分解因式正确的是( )| A. | x2-1+x=(x+1)(x-1)+x | B. | (m+n)2-6(m+n)+9=(m+n-3)(m+n+3) | ||
| C. | x6-10x3-25=(x3-5)2 | D. | -1+x4=(x+1)(x-1)(x2+1) |
分析 分别利用平方差以及完全平方公式分解因式进而得出答案.
解答 解:A、x2-1+x=(x+1)(x-1)+x不是因式分解,故此选项错误;
B、(m+n)2-6(m+n)+9=(m+n-3)2,故此选项错误;
C、x6-10x3-25无法因式分解,故此选项错误;
D、-1+x4=(x+1)(x-1)(x2+1),正确.
故选:D.
点评 此题主要考查了完全平方公式以及平方差公式的应用,熟练应用公式是解题关键.

练习册系列答案
相关题目
10. 如图,数轴上点N表示的数可能是( )
如图,数轴上点N表示的数可能是( )
 如图,数轴上点N表示的数可能是( )
如图,数轴上点N表示的数可能是( )| A. | $\sqrt{10}$ | B. | $\sqrt{6}$ | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
8.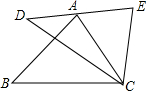 如图,点A在DE上,AC=CE,∠DAB=∠BCD=∠ACE,则AB与DE的数量关系为( )
如图,点A在DE上,AC=CE,∠DAB=∠BCD=∠ACE,则AB与DE的数量关系为( )
 如图,点A在DE上,AC=CE,∠DAB=∠BCD=∠ACE,则AB与DE的数量关系为( )
如图,点A在DE上,AC=CE,∠DAB=∠BCD=∠ACE,则AB与DE的数量关系为( )| A. | AB=DE | B. | AB>DE | C. | AB<DE | D. | 不能确定 |
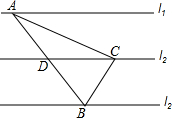 已知,如图,直线l1,l2,l3是三条等距的平行线,将一块含30°角的直角三角板如图放置,使直角顶点C落在l2上,另两个顶点A与B刚好分落在l1与l3上,AB与l2交于点D
已知,如图,直线l1,l2,l3是三条等距的平行线,将一块含30°角的直角三角板如图放置,使直角顶点C落在l2上,另两个顶点A与B刚好分落在l1与l3上,AB与l2交于点D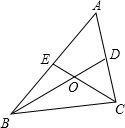 已知:如图,△ABC中,中线BD和中线CE相交于点O,求证:BO=2DO.
已知:如图,△ABC中,中线BD和中线CE相交于点O,求证:BO=2DO.