题目内容
9.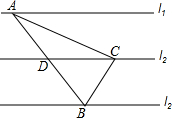 已知,如图,直线l1,l2,l3是三条等距的平行线,将一块含30°角的直角三角板如图放置,使直角顶点C落在l2上,另两个顶点A与B刚好分落在l1与l3上,AB与l2交于点D
已知,如图,直线l1,l2,l3是三条等距的平行线,将一块含30°角的直角三角板如图放置,使直角顶点C落在l2上,另两个顶点A与B刚好分落在l1与l3上,AB与l2交于点D(1)求证:AD=BD;
(2)若BD=2,求直线l1,l2,l3之间的距离.
分析 (1)过点C作l2的垂线分别交l1与l3于点E、F,由平行线分线段成比例可直接得出结论;
(2)由(1)知D是AB中点,再加上∠A=30°,可得出三角形BCD是等边三角形,线l1,l2,l3之间的距离就是等边三角形的高.
解答 解:(1)过点C作l2的垂线分别交l1与l3于点E、F,如图,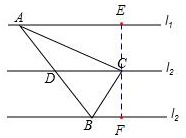
∵l1∥l2∥l3,且EC=CF,
∴$\frac{AD}{DB}=\frac{EC}{CF}=1$,
∴AD=BD;
(2)∵∠A=30°,∠ACB=90°,AD=BD,
∴CD=BD=BC,
即:△BCD是等边三角形,
∴CF=BC•sin60°=$\frac{\sqrt{3}}{2}BC=\frac{\sqrt{3}}{2}BD$=$\sqrt{3}$.
即:l1,l2,l3之间的距离为$\sqrt{3}$.
点评 本题主要考查了平行线平线段成比例、含30°的直角三角形的性质、直角三角形斜边中线性质、特殊角的三角函数等知识点,难度不大.第(1)问其实体现了一种证明线段相等的方法,也体现了平行线具有转移线段关系的重要功能,要引起重视,并能将这里的方法自觉运用到其也相关题的解答当中.

练习册系列答案
相关题目
19.下列分解因式正确的是( )
| A. | x2-1+x=(x+1)(x-1)+x | B. | (m+n)2-6(m+n)+9=(m+n-3)(m+n+3) | ||
| C. | x6-10x3-25=(x3-5)2 | D. | -1+x4=(x+1)(x-1)(x2+1) |
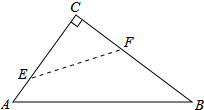 如图,在Rt△ABC中,∠C=90°,翻折∠C,使点C落在斜边AB上某一点D处,折痕为EF(点E,F分别在边AC,BC上),给出以下判断:
如图,在Rt△ABC中,∠C=90°,翻折∠C,使点C落在斜边AB上某一点D处,折痕为EF(点E,F分别在边AC,BC上),给出以下判断: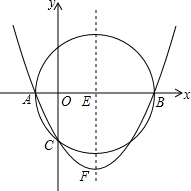 如图,已知以E(3,0)为圆心,以5为半径的⊙E与x轴交于A,B两点,与y轴交于C点,抛物线y=ax2+bx+c经过A,B,C三点,顶点为F.
如图,已知以E(3,0)为圆心,以5为半径的⊙E与x轴交于A,B两点,与y轴交于C点,抛物线y=ax2+bx+c经过A,B,C三点,顶点为F. 如图,是“太阳超市”中某品牌洗发水的价格标签,请你在横线上填写它的原价20元.
如图,是“太阳超市”中某品牌洗发水的价格标签,请你在横线上填写它的原价20元.