题目内容
4.计算下列各式(1)$\frac{5y}{4x}•\frac{8x}{-15y^2}$÷$\frac{-y}{x}$
(2)$\frac{x}{{{x^2}-1}}+\frac{3x+1}{{{x^2}-1}}$+$\frac{2x+3}{{1-{x^2}}}$.
分析 ①首先确定符号,把除法转化为乘法,然后进行乘法计算即可;
②首先利用同分母的分式加减法则计算,然后进行化简即可.
解答 解:①原式=$\frac{5y}{4x}$•$\frac{8x}{15{y}^{2}}$•$\frac{x}{y}$=$\frac{2x}{3{y}^{2}}$;
②原式=$\frac{x}{(x+1)(x-1)}$+$\frac{3x+1}{(x+1)(x-1)}$-$\frac{2x+3}{(x+1)(x-1)}$
=$\frac{x+(3x+1)-(2x+3)}{(x+1)(x-1)}$
=$\frac{2x-2}{(x+1)(x-1)}$
=$\frac{2(x-1)}{(x+1)(x-1)}$
=$\frac{2}{x+1}$.
点评 本题主要考查分式的混合运算,通分、因式分解和约分是解答的关键.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
19.下列分解因式正确的是( )
| A. | x2-1+x=(x+1)(x-1)+x | B. | (m+n)2-6(m+n)+9=(m+n-3)(m+n+3) | ||
| C. | x6-10x3-25=(x3-5)2 | D. | -1+x4=(x+1)(x-1)(x2+1) |
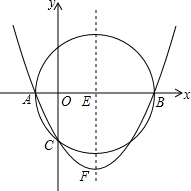 如图,已知以E(3,0)为圆心,以5为半径的⊙E与x轴交于A,B两点,与y轴交于C点,抛物线y=ax2+bx+c经过A,B,C三点,顶点为F.
如图,已知以E(3,0)为圆心,以5为半径的⊙E与x轴交于A,B两点,与y轴交于C点,抛物线y=ax2+bx+c经过A,B,C三点,顶点为F.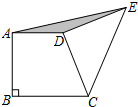 如图,在直角梯形ABCD中,AD∥BC,AB⊥BC,AD=4,BC=6.以D为直角顶点CD为腰向外作等腰Rt△CDE,连接AE,则△ADE的面积是4.
如图,在直角梯形ABCD中,AD∥BC,AB⊥BC,AD=4,BC=6.以D为直角顶点CD为腰向外作等腰Rt△CDE,连接AE,则△ADE的面积是4.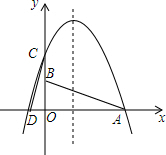 如图,已知,A点坐标是(3,0),B点坐标是(0,1),将△AOB绕点O逆时针旋转90°得到△COD,A、B旋转后的对应点分别为C和D,抛物线y=-x2+bx+c经过C、D两点.
如图,已知,A点坐标是(3,0),B点坐标是(0,1),将△AOB绕点O逆时针旋转90°得到△COD,A、B旋转后的对应点分别为C和D,抛物线y=-x2+bx+c经过C、D两点.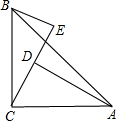 如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于点D,AD=3.1cm,DE=1.8cm,求BE的长.
如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于点D,AD=3.1cm,DE=1.8cm,求BE的长.