题目内容
5.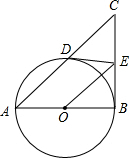 如图,在Rt△ABC中,∠ABC=90°,以AB为直径的⊙O与AC边交于点D,过点D作⊙O的切线交BC于点E,连接OE
如图,在Rt△ABC中,∠ABC=90°,以AB为直径的⊙O与AC边交于点D,过点D作⊙O的切线交BC于点E,连接OE(1)证明OE∥AD;
(2)①当∠BAC=45°时,四边形ODEB是正方形.
②当∠BAC=30°时,AD=3DE.
分析 (1)连接OD,证明Rt△ODE≌Rt△OBE得到∠BOE=$\frac{1}{2}$∠DOB,根据半径相等得到∠A=$\frac{1}{2}$∠DOB,根据平行线的判定证明OE∥AD;
(2)①根据正方形的性质和平行线的性质可得结论;
②作OF⊥AD于F,根据垂径定理和锐角三角函数的知识计算得到答案.
解答 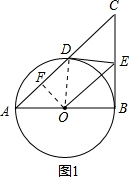 解:(1)连接OD,
解:(1)连接OD,
∵DE是⊙O的切线,
∴OD⊥DE,
在Rt△ODE和Rt△OBE中,
$\left\{\begin{array}{l}{OD=OB}\\{OE=OE}\end{array}\right.$,
∴Rt△ODE≌Rt△OBE,
∴∠BOE=$\frac{1}{2}$∠DOB,
∵OA=OD,
∴∠A=$\frac{1}{2}$∠DOB,
∴∠BOE=∠A,
∴OE∥AD;
(2)①当四边形ODEB是正方形时,BO=BE,
∴∠BOE=45°,
∵OE∥AD,
∴∠BAC=45°;
②当∠BAC=30°时,AD=3DE,
证明:作OF⊥AD于F,
由垂径定理可知,AF=DF=$\frac{1}{2}$AD,
∵∠BAC=30°,
∴∠ODF=∠DOE=30°,
∴OD=$\frac{DF}{cos30°}$=$\frac{\sqrt{3}}{3}$AD,
OD=$\frac{DE}{tan30°}$=$\sqrt{3}$DE,
∴AD=3DE.
点评 本题考查的是切线的性质和全等三角形的判定和性质以及锐角三角函数的概念,正确找出辅助线、灵活运用切线的性质在直角三角形中正确运用三角函数的概念是解题的关键.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
7.下列图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  平行四边形 | B. |  圆 | C. |  正五边形 | D. |  等腰三角形 |
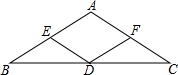 如图,已知△ABC中,AB=AC,E,D,F分别是边AB,BC,AC的中点.
如图,已知△ABC中,AB=AC,E,D,F分别是边AB,BC,AC的中点.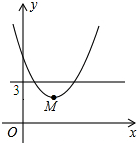 在平面直角坐标系中,点M是直线y=3与x轴之间的一个动点,且点M是抛物线y=$\frac{1}{5}$x2+bx+c的顶点,则方程$\frac{1}{5}$x2+bx+c=2的解的个数是0,1或2.
在平面直角坐标系中,点M是直线y=3与x轴之间的一个动点,且点M是抛物线y=$\frac{1}{5}$x2+bx+c的顶点,则方程$\frac{1}{5}$x2+bx+c=2的解的个数是0,1或2.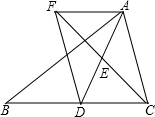 已知:如图,在△ABC中,D是BC边上的一点,连结AD,取AD的中点E,过点A作BC的平行线与CE的延长线交于点F,连结DF.求证:AF=DC.
已知:如图,在△ABC中,D是BC边上的一点,连结AD,取AD的中点E,过点A作BC的平行线与CE的延长线交于点F,连结DF.求证:AF=DC.