题目内容
14.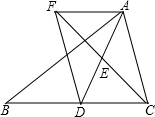 已知:如图,在△ABC中,D是BC边上的一点,连结AD,取AD的中点E,过点A作BC的平行线与CE的延长线交于点F,连结DF.求证:AF=DC.
已知:如图,在△ABC中,D是BC边上的一点,连结AD,取AD的中点E,过点A作BC的平行线与CE的延长线交于点F,连结DF.求证:AF=DC.
分析 因为AF∥DC,E为AD的中点,即可根据AAS证明△AEF≌△DEC,故有AF=DC.
解答 证明:∵AF∥DC,
∴∠AFE=∠DCE,
又∵∠AEF=∠DEC(对顶角相等),AE=DE(E为AD的中点),
在△AEF与△DEC中,$\left\{\begin{array}{l}{∠AFE=∠DCE}\\{∠AEF=∠DEC}\\{AE=DE}\end{array}\right.$,
∴△AEF≌△DEC(AAS),
∴AF=DC.
点评 本题考查全等三角形的判定与性质.在应用全等三角形的判定时,要注意三角形间的公共边、公共角以及对顶角,必要时添加适当辅助线构造三角形.

练习册系列答案
相关题目
2.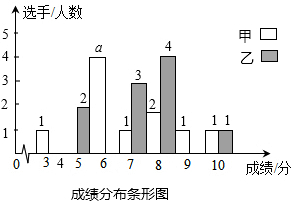 某县为选派一个代表队(10名选手)参加市举办的纪念抗战胜利70周年知识竞赛,现有甲、乙两支代表队(各10名选手)参加县里预选,预选时选手得分满分为10分,且选手得分均为整数,成绩达6分及以上为合格,9分或10分为优秀.各队选手成绩分布的条形统计图和成绩统计分析表如下:
某县为选派一个代表队(10名选手)参加市举办的纪念抗战胜利70周年知识竞赛,现有甲、乙两支代表队(各10名选手)参加县里预选,预选时选手得分满分为10分,且选手得分均为整数,成绩达6分及以上为合格,9分或10分为优秀.各队选手成绩分布的条形统计图和成绩统计分析表如下:
成绩统计分析表
(1)请依据图表中的数据,求出条形图中a的值;
(2)写出表中m、n的值;
(3)有人说甲队的合格率、优秀率均高于乙队,所以应选派甲队参加市赛,但也有人认为乙队成绩比甲队好.请给出两条支持乙队代表县里参加市赛的理由.
 某县为选派一个代表队(10名选手)参加市举办的纪念抗战胜利70周年知识竞赛,现有甲、乙两支代表队(各10名选手)参加县里预选,预选时选手得分满分为10分,且选手得分均为整数,成绩达6分及以上为合格,9分或10分为优秀.各队选手成绩分布的条形统计图和成绩统计分析表如下:
某县为选派一个代表队(10名选手)参加市举办的纪念抗战胜利70周年知识竞赛,现有甲、乙两支代表队(各10名选手)参加县里预选,预选时选手得分满分为10分,且选手得分均为整数,成绩达6分及以上为合格,9分或10分为优秀.各队选手成绩分布的条形统计图和成绩统计分析表如下:成绩统计分析表
| 成绩/队别 | 平均分 | 中位数 | 方差 | 合格率% | 优秀率% |
| 甲队 | 6.9 | m | 3.41 | 9 | n |
| 乙队 | 6.8 | x-1 | 3.25 | 8 | x |
(2)写出表中m、n的值;
(3)有人说甲队的合格率、优秀率均高于乙队,所以应选派甲队参加市赛,但也有人认为乙队成绩比甲队好.请给出两条支持乙队代表县里参加市赛的理由.
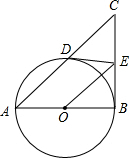 如图,在Rt△ABC中,∠ABC=90°,以AB为直径的⊙O与AC边交于点D,过点D作⊙O的切线交BC于点E,连接OE
如图,在Rt△ABC中,∠ABC=90°,以AB为直径的⊙O与AC边交于点D,过点D作⊙O的切线交BC于点E,连接OE 如图,矩形ABCD中,AB=6,AD=8,点E在边AD上,且AE:ED=1:3.动点P从点A出发,沿AB 运动到点B停止.过点E作EF⊥PE交射线BC于点F,设M是线段EF的中点,则在点P运动的整个过程中,点M运动路线的长为9.
如图,矩形ABCD中,AB=6,AD=8,点E在边AD上,且AE:ED=1:3.动点P从点A出发,沿AB 运动到点B停止.过点E作EF⊥PE交射线BC于点F,设M是线段EF的中点,则在点P运动的整个过程中,点M运动路线的长为9. 如图,AE是△ABC的外角平分线,∠B=∠C,试说明AE∥BC的理由.
如图,AE是△ABC的外角平分线,∠B=∠C,试说明AE∥BC的理由.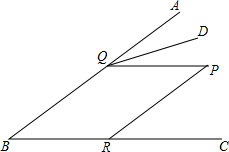 如图,点P在∠ABC内,点Q,R分别在∠ABC的边BA,BC上,QD平分∠AQP,连接PQ,PR.若∠PRC=∠B,∠P=50°,求∠PQD的度数.
如图,点P在∠ABC内,点Q,R分别在∠ABC的边BA,BC上,QD平分∠AQP,连接PQ,PR.若∠PRC=∠B,∠P=50°,求∠PQD的度数.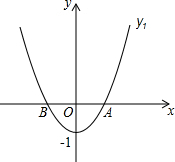 如图,在平面直角坐标系中,抛物线y1=x2-1与x轴交于点A和点B(点A在点B的右侧),抛物线y2的解析式为y2=$\frac{1}{1-n}$(x-n)2+n-1(n≠1,直线y3的解析式为y3=x-2.
如图,在平面直角坐标系中,抛物线y1=x2-1与x轴交于点A和点B(点A在点B的右侧),抛物线y2的解析式为y2=$\frac{1}{1-n}$(x-n)2+n-1(n≠1,直线y3的解析式为y3=x-2.