题目内容
19. 如图,已知:AB∥CD∥EF,OC:CE=2:3,OA:OD=3:2,OB=6cm,OD=4cm.求线段BE、AF的长.
如图,已知:AB∥CD∥EF,OC:CE=2:3,OA:OD=3:2,OB=6cm,OD=4cm.求线段BE、AF的长.
分析 由于AB∥CD,所以△AOB∽△COD,所以$\frac{OA}{OD}=\frac{OB}{OC}$,从而可求出OC=4cm,OA=6cm,由于CD∥EF,所以△COD∽△EOF,从而$\frac{OC}{OE}$=$\frac{OD}{OF}$,从而可求出OF=10cm,OE=10cm.
解答 解:∵AB∥CD,
∴△AOB∽△COD,
∴$\frac{OA}{OD}=\frac{OB}{OC}$,
∵OB=6cm,OD=4cm
∴OC=4cm,OA=6cm,
∵CD∥EF,
∴△COD∽△EOF
∴$\frac{OC}{OE}$=$\frac{OD}{OF}$,
∵$\frac{OC}{CE}=\frac{2}{3}$,
∴$\frac{OC}{OE}=\frac{2}{5}$,
∴OF=10cm,OE=10cm
∴BE=OB+OE=6+10=16cm,
AF=OA+OF=6+10=16cm,
点评 本题考查相似三角形的性质与判定,解题的关键是熟练运用相似三角形的性质与判定,本题属于基础题型.

练习册系列答案
相关题目
14.某小区为了营造优雅宜居人文环境,积极推进小区绿地、主题公园、休闲场地建设,小区利用甲种花卉和乙种花卉搭配成A,B两种园艺造型摆放在中央大道两侧,搭配数量如下表所示:
(1)已知搭配一个A种园艺造型和一个B种园艺造型共需500元.若园林局搭配A种园艺造型32个,B种园艺造型18个共投入11800元.则A、B两种园艺造型的单价分别是多少元?
(2)如果搭配A、B两种园艺造型共50个,某校学生课外小组承接了搭配方案的设计,其中甲种花卉不超过3490盆,乙种花卉不超过2950盆,问符合题意的搭配方案有几种?请你帮忙设计出来.
| 甲种花卉(盆) | 乙种花卉(盆) | |
| A种园艺造型(个) | 80盆 | 40盆 |
| B种园艺造型(个) | 50盆 | 90盆 |
(2)如果搭配A、B两种园艺造型共50个,某校学生课外小组承接了搭配方案的设计,其中甲种花卉不超过3490盆,乙种花卉不超过2950盆,问符合题意的搭配方案有几种?请你帮忙设计出来.
11.放暑假了,小李同学勤工俭学购进一批矿泉水和运动饮料在运动场进行销售,其进价与售价如下表:
(1)若小李同学购进矿泉水和运动饮料共30瓶,用去了67.5元,并且全部售完,问小李同学在该买卖中赚了多少钱?
(2)为了进一步满足同学们的需求,小李同学决定用不超过200元的资金购进矿泉水和运动饮料共100瓶,问最多购进多少瓶运动饮料?
(3)小李同学赚钱后,为了回报社会,买了一批书籍送给贫困山区的孩子,如果分给每位孩子4本书,那么剩下28本书;如果分给每位孩子5本书,那么最后一位孩子分得的书不足4本,但至少1本,则小李同学买了多少本书?
| 进价(元/瓶) | 售价(元/瓶) | |
| 矿泉水 | 0.75 | 2 |
| 运动饮料 | 3 | 4 |
(2)为了进一步满足同学们的需求,小李同学决定用不超过200元的资金购进矿泉水和运动饮料共100瓶,问最多购进多少瓶运动饮料?
(3)小李同学赚钱后,为了回报社会,买了一批书籍送给贫困山区的孩子,如果分给每位孩子4本书,那么剩下28本书;如果分给每位孩子5本书,那么最后一位孩子分得的书不足4本,但至少1本,则小李同学买了多少本书?
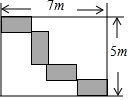 如图是某居民小区内的矩形工地,工地里有四块相同的小矩形绿化区域.小矩形的边都与工地的边平行,每个矩形由顶点连接,求小矩形的长和宽.
如图是某居民小区内的矩形工地,工地里有四块相同的小矩形绿化区域.小矩形的边都与工地的边平行,每个矩形由顶点连接,求小矩形的长和宽.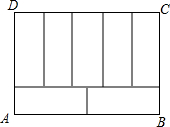 如图,周长为68cm的长方形ABCD被分成7个相同的矩形,求长方形ABCD的面积.
如图,周长为68cm的长方形ABCD被分成7个相同的矩形,求长方形ABCD的面积. 如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.