题目内容
15.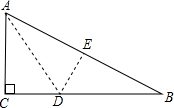 如图,一中江县进行纸片,AC=6cm,AB=10cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于( )
如图,一中江县进行纸片,AC=6cm,AB=10cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于( )| A. | 3cm | B. | 5cm | C. | 3$\sqrt{5}$cm | D. | 9$\sqrt{5}$cm |
分析 先根据勾股定理求出BC的长,再根据图形翻折变换的性质得出△AED≌△ACD;进而得到AE=AC=6,DE=CD;根据勾股定理求出AB=10;再次利用勾股定理列出关于线段CD的方程,问题即可解决.
解答 解:设CD=x,
∵AC=6cm,AB=10cm,∠C=90°,
∴BC=$\sqrt{{AB}^{2}-{AC}^{2}}$=$\sqrt{{10}^{2}-{6}^{2}}$=8cm.
∵△ADE由△ADC翻折而成,
∴△AED≌△ACD,
∴AE=AC=6,DE=CD=x,∠AED=∠C=90°,
∴BE=10-6=4,BD=8-x;
由勾股定理得:
(8-x)2=42+x2,
解得:x=3(cm).
故选A.
点评 本题考查的是翻折变换,熟知图形翻折不变性的性质是解答此题的关键.

练习册系列答案
相关题目
5.下列命题正确的是( )
| A. | 对角线互相垂直的四边形是菱形 | |
| B. | 有三个角是直角的四边形是矩形 | |
| C. | 有两条边相等的四边形是平行四边形 | |
| D. | 四条边都相等的平行四边形是正方形 |
4.为了帮助农村贫困家庭子女完成初中学业,国家给他们免费提供教科书,下表是某中学免费提供教科书补助的部分情况:
求获得免费提供教科书补助的七年级和八年级的人数.
| 年级 项目 | 七 | 八 | 九 | 合计 |
| 每人免费补助金额/元 | 109 | 94 | 47.5 | - |
| 人数/人 | 40 | 120 | ||
| 免费补助金额/元 | 1900 | 10095 |
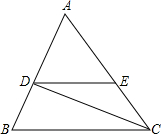 已知:如图,CD是∠ACB的平分线,∠ACB=48°,∠BDC=82°,DE∥BC.
已知:如图,CD是∠ACB的平分线,∠ACB=48°,∠BDC=82°,DE∥BC.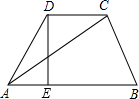 如图,在梯形ABCD中,DC∥AB,DE⊥AB,DC=2,AC=$\sqrt{19}$,∠DAE=60°,则DE=$\frac{3\sqrt{3}}{2}$.
如图,在梯形ABCD中,DC∥AB,DE⊥AB,DC=2,AC=$\sqrt{19}$,∠DAE=60°,则DE=$\frac{3\sqrt{3}}{2}$.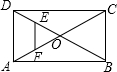 如图,在矩形ABCD中,对角线AC和BD相交于点O,点E、F分别是DO、AO的中点.若AB=8cm,BC=4cm,则△OEF的周长为(2$\sqrt{5}$+2)cm.
如图,在矩形ABCD中,对角线AC和BD相交于点O,点E、F分别是DO、AO的中点.若AB=8cm,BC=4cm,则△OEF的周长为(2$\sqrt{5}$+2)cm. 已知2y-3与-3x-1成正比例,且x=2时,y=5.
已知2y-3与-3x-1成正比例,且x=2时,y=5.