题目内容
18. 如图,我南海某海域A处有一艘捕鱼船在作业时突遇特大风浪,船长马上向我国渔政搜救中心发出求救信号,此时一艘渔政船正巡航到捕鱼船正西方向的B处,该渔政船收到渔政求救中心指令后前去救援,但两船之间有大片暗礁,无法直线到达,于是决定马上调整方向,先向北偏东60°方向以每小时30海里的速度航行半小时到达C处,同时捕鱼船低速航行到A点的正北1.5海里D处,渔政船航行到点C处时测得点D在南偏东53°方向上.
如图,我南海某海域A处有一艘捕鱼船在作业时突遇特大风浪,船长马上向我国渔政搜救中心发出求救信号,此时一艘渔政船正巡航到捕鱼船正西方向的B处,该渔政船收到渔政求救中心指令后前去救援,但两船之间有大片暗礁,无法直线到达,于是决定马上调整方向,先向北偏东60°方向以每小时30海里的速度航行半小时到达C处,同时捕鱼船低速航行到A点的正北1.5海里D处,渔政船航行到点C处时测得点D在南偏东53°方向上.(1)求CD两点的距离;
(2)渔政船决定再次调整航向前去救援,若两船航速不变,并且在点E处相会合,求∠ECD的正弦值.
(参考数据:sin53°≈$\frac{4}{5}$,cos53°≈$\frac{3}{5}$,tan53°≈$\frac{4}{3}$)
分析 (1)过点C、D分别作CG⊥AB,DF⊥CG,垂足分别为G,F,根据直角三角形的性质得出CG,再根据三角函数的定义即可得出CD的长;
(2)如图,设渔政船调整方向后t小时能与捕渔船相会合,由题意知CE=30t,DE=1.5×2×t=3t,∠EDC=53°,过点E作EH⊥CD于点H,根据三角函数表示出EH,在Rt△EHC中,根据正弦的定义求值即可.
解答  解:(1)过点C、D分别作CG⊥AB,DF⊥CG,垂足分别为G,F,
解:(1)过点C、D分别作CG⊥AB,DF⊥CG,垂足分别为G,F,
∵在Rt△CGB中,∠CBG=90°-60°=30°,
∴CG=$\frac{1}{2}$BC=$\frac{1}{2}$×(30×$\frac{1}{2}$)=7.5,
∵∠DAG=90°,
∴四边形ADFG是矩形,
∴GF=AD=1.5,
∴CF=CG-GF=7.5-1.5=6,
在Rt△CDF中,∠CFD=90°,
∵∠DCF=53°,
∴COS∠DCF=$\frac{CF}{CD}$,
∴CD=$\frac{CF}{COS53°}$=$\frac{6}{\frac{3}{5}}$=10(海里).
答:CD两点的距离是10;
(2)如图,设渔政船调整方向后t小时能与捕渔船相会合,
由题意知CE=30t,DE=1.5×2×t=3t,∠EDC=53°,
过点E作EH⊥CD于点H,则∠EHD=∠CHE=90°,
∴sin∠EDH=$\frac{EH}{ED}$,
∴EH=EDsin53°=3t×$\frac{4}{5}$=$\frac{12}{5}$t,
∴在Rt△EHC中,sin∠ECD=$\frac{EH}{CE}$=$\frac{\frac{12}{5}t}{30t}$=$\frac{2}{25}$.
答:sin∠ECD=$\frac{2}{25}$.
点评 考查了解直角三角形的应用-方向角问题,此题是一道方向角问题,结合航海中的实际问题,将解直角三角形的相关知识有机结合,体现了数学应用于实际生活的思想.

| A. | $\frac{1}{{x}^{2}+1}$ | B. | $\frac{x}{2x+1}$ | C. | $\frac{1}{{x}^{2}}$ | D. | $\frac{x-5}{x}$ |
 如图,点O、A在数轴上表示的数分别是0,0.1,将线段OA分成100等份,其分点由左向右依次为M1,M2…M99,再将线段OM1分成100等份,其分点由左向右依次为N1,N2,…N99,则点N15所表示的数用科学记数法表示为1.5×10-4.
如图,点O、A在数轴上表示的数分别是0,0.1,将线段OA分成100等份,其分点由左向右依次为M1,M2…M99,再将线段OM1分成100等份,其分点由左向右依次为N1,N2,…N99,则点N15所表示的数用科学记数法表示为1.5×10-4. 如图,已知△ABC和点O,画出△DEF,使△DEF和△ABC关于点O成中心对称.(画出图形并写出解答过程)
如图,已知△ABC和点O,画出△DEF,使△DEF和△ABC关于点O成中心对称.(画出图形并写出解答过程)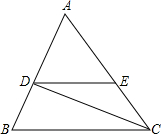 已知:如图,CD是∠ACB的平分线,∠ACB=48°,∠BDC=82°,DE∥BC.
已知:如图,CD是∠ACB的平分线,∠ACB=48°,∠BDC=82°,DE∥BC.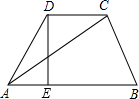 如图,在梯形ABCD中,DC∥AB,DE⊥AB,DC=2,AC=$\sqrt{19}$,∠DAE=60°,则DE=$\frac{3\sqrt{3}}{2}$.
如图,在梯形ABCD中,DC∥AB,DE⊥AB,DC=2,AC=$\sqrt{19}$,∠DAE=60°,则DE=$\frac{3\sqrt{3}}{2}$. 已知2y-3与-3x-1成正比例,且x=2时,y=5.
已知2y-3与-3x-1成正比例,且x=2时,y=5.